原链接:https://www.ambionics.io/blog/php-mt-rand-prediction
只用两个输出值破解mt_rand函数,无需爆破
介绍
当在对一个旧网站做渗透测试时,我们遇到了一些很久没见到过的代码:1
2
3
4
5
6
7
8<?php
function resetPassword($email)
{
[...]
$superSecretToken = md5($email . ':' . mt_rand());
[...]
$this->sendEmailWithResetToken($email, $superSecretToken);
}
利用PHP实现Mersenne Twister(一种伪随机数生成器),输出生成了一个被认为是秘密且不可猜测的token。
在过去十年里,一场因为其内部对话(通信/处理?)的美好时代里关于PRNG(pseudorandom number generator伪随机数生成器)的预测,以及它在过去十年早期产生的大量文章和工具。(太奇怪了这句话)。当时,许多应用程序使用rand()或mt_rand()来生成秘密令牌或密码。这些函数被标记为密码不安全的,因此不应该用于密码目的。为了预测这些值,你必须找到种子,也就是所有这些值的最初值。大家一致认为,您需要获得整个内部状态(mt_rand()的624个值),或者使用这些值的一部分来对种子进行bruteforce处理。
然而,我们的一名研究人员坚持认为,仅使用mt_rand()函数的两个输出就可以恢复Mersenne Twister算法的种子,而且不需要任何形式的暴力破解。然而,我们找不到任何支持这一理论的资料,他关于这个问题的笔记早就丢失了。
在对这些数据进行了一番分析之后,在PRNG预测闹剧结束多年之后,我们证明了他是对的。看在过去的份上,我们现在将演示如何做到这一点。
只用两个输出值和一点数学知识破解PHP的Mersenne Twister算法
使用mt_rand()函数在生成随机数的第一步,是使用一个种子,以无符号整型的数据类型生成一个624个值的状态数组。通过调用mt_srand($seed),或者在通过PHP请求第一个随机数时自动完成。在这之后,每次调用mt_rand()都将获取下一个状态值,并将其打乱,在将其返回给用户。
所有事情发生在文件ext/standard/mt_rand.c中对于较新的PHP版本(PHP7+),或者文件ext/standard/rand.c中,对于更久的PHP版本(PHP5-)。
知道种子的值使您能够预测PRNG生成的每个数字,直到再次调用mt_srand()为止。因此,从mt_rand()的一个或多个值生成的秘密随机值将不再是秘密的,从而导致明显的安全问题。
随机数生成过程分为三个步骤:
1.通过种子的模乘法生成一个初始化的状态数组
2.将状态值打乱得到一个打乱的状态数组
3.调用mt_rand()时,返回一个修改后的打乱的状态值
对于每个步骤,我们将展示代码,简要描述其工作方式,然后介绍如何从输出到输入。
注意:PHP7+对负责生成打乱状态的代码进行了一些更改(请参阅mt_randl .c中定义的twist和twist_php #)。这个变化不大,因为我们可以通过算法的每个变化得到种子。在这里,我们主要关注最初的实现,twist_php。底部提供的脚本可以处理两个版本。
种子到初始状态
1 | #define MT_N (624) |
创建了一个包含624个值的初始状态数组。第一种状态是种子。每个后续的状态值都是由前一个状态值生成的。
现在,如果我们知道这些状态值中的任何一个,比如state[123],我们能否推出state{0},也就是种子?
python版本的代码是:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16N = 624
M = 397
MAX = 0xffffffff
STATE_MULT = 1812433253
def php_mt_initialize(seed):
"""Creates the initial state array from a seed.
"""
state = [None] * N
state[0] = seed & 0xffffffff;
for i in range(1, N):
r = state[i-1]
state[i] = ( STATE_MULT * ( r ^ (r >> 30) ) + i ) & MAX
return state
由于值是通过迭代生成的,所以我们需要做的第一件事是尝试从i和state[i]中找出state[i-1]。然后我们可以在i- 1,i -2上重复这个操作,直到我们找到state[0],也就是种子。用S代表状态,i代表区间[1,624],我们有: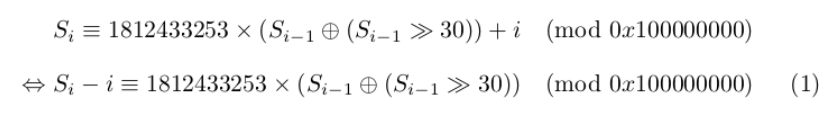
我们可以计算出1812433253对0x100000000的模逆元:
在python中,我们可以得到:1
2
3
4
5
6
7
8
9
10
11
12
13STATE_MULT_INV = 2520285293
MAX = 0xffffffff
def _undo_php_mt_initialize(s, i):
s = (STATE_MULT_INV * (s - i)) & MAX
return s ^ s >> 30
def undo_php_mt_initialize(s, p):
"""From an initial state value `s` at position `p`, find out seed.
"""
for i in range(p, 0, -1):
s = _undo_php_mt_initialize(s, i)
return s
这意味着如果我们得到任何初始状态值,我们可以计算任何其他状态值,以及种子。
从初始状态到打乱状态
1 | #define hiBit(u) ((u) & 0x80000000U) /* mask all but highest bit of u */ |
初始状态数组通过混合值进行置乱,从而产生一个新的状态,即置乱状态。前226 (N-M)个值的计算与后面的值不同。在python中,我们有:1
2
3
4
5
6
7
8
9
10
11
12
13
14N = 624
M = 397
def php_mt_reload(s):
for i in range(0, N - M):
s[i] = _twist(s[i+M], s[i], s[i+1])
for i in range(N - M, N - 1):
s[i] = _twist(s[i+M-N], s[i], s[i+1])
def _twist_php(m, u, v):
"""Emulates the `twist` #define.
"""
mask = 0x9908b0df if u & 1 else 0
return m ^ (((u & 0x80000000) | (v & 0x7FFFFFFF)) >> 1) ^ mask
在这里,我们会证明我们可以从两个打乱的状态中推导出一个初始状态。
state[0]和state[227]之间有关系。如果我们用s来命名初始状态数组,用S来命名新的置乱的状态数组,我们有:1
2
3
4S[227] = _twist(S[227 - 227], s[227], s[228])
<=> S[227] = _twist(S[0], s[227], s[228])
<=> S[227] = S[0] ^ (((s[227] & 0x80000000) | (s[228] & 0x7FFFFFFF)) >> 1) ^ (0x9908b0df if s[227] & 1 else 0)
<=> S[227] ^ S[0] = (((s[227] & 0x80000000) | (s[228] & 0x7FFFFFFF)) >> 1) ^ (0x9908b0df if s[227] & 1 else 0)
作为一个攻击者,如果我们知道了置乱状态S[0]和S[227],以及它们的XOR,我们就会得到很多关于初始状态s[228]的信息,还有一些关于s[227]的信息。如果我们用X表示S[227] ^ S[0],我们有:
因为XOR表达式的左部分是右移的,所以它的MSB总是空的。因此,MSB(0x9908b0df)只由右边的掩码来决定,因为MSB(0x9908b0df)已经设置好了。因此,MSB(X) = LSB(s[227]),如果X有掩码,我们可以把它去掉。
然后,BIT(s[227], 31) = BIT(X, 30)。
其余的值是来自s[228]的位,即来自30到1的位。
*MSB:最高有效位 LSB:最低有效位
综上所述,我们有:
> 初始状态值s[227]的MSB和LSB
> 初始状态值s[228]从30到1的位
因此,我们有4个可能的s值[228]。但是,由于我们也知道s[227]的一些位,我们可以从s[228]的四个可能值中每一个计算一个候选s227,并验证得到的s[227]值的 LSB和MSB是否与我们已有的值匹配。此外,我们可以获得与候选状态s[228]相关联的种子(同样,参考第一部分了解如何关联)。然后我们可以使用这个种子来重新生成一个状态,并检查它是否匹配S[0]。下面是python代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41def undo_php_mt_reload(S000, S227):
# m S000
# u S227
# v S228
X = S000 ^ S227
# This means the mask was applied, and as such that S227's LSB is 1
s22X_0 = bv(X, 31)
# remove mask if present
if s22X_0:
X ^= 0x9908b0df
# Another easy guess
s227_31 = bv(X, 30)
# remove bit if present
if s227_31:
X ^= 1 << 30
# We're missing bit 0 and bit 31 here, so we have to try every possibility
s228_1_30 = (X << 1)
for s228_0 in range(2):
for s228_31 in range(2):
s228 = s228_0 | s228_31 << 31 | s228_1_30
# Check if the results are consistent with the known bits of s227
s227 = _undo_php_mt_initialize(s228, 228)
if bv(s227, 0) != s22X_0:
continue
if bv(s227, 31) != s227_31:
continue
# Check if the guessed seed yields S000 as its first scrambled state
rand = undo_php_mt_initialize(s228, 228)
state = php_mt_initialize(rand)
php_mt_reload(state)
if not S000 == state[0]:
continue
return rand
return None
为了推导出原始种子,我们使用了置乱状态S[0]和S[227]之间的关系。可以看到,这种关系对于任何由226个值分隔的状态值都是有效的。因此,知道S[i]和S[i+227]这两个状态值,以及它们的偏移量i,我们就可以恢复种子。
现在我们可以检查mt_rand() PRNG的最后一步。
置乱状态值到mt rand()输出
当我们调用mt_rand()时,PHP从打乱的状态数组中获取一个值,稍微摆弄一下(作者在卖萌吗),然后返回它。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35PHP_FUNCTION(mt_rand)
{
zend_long min;
zend_long max;
int argc = ZEND_NUM_ARGS();
if (argc == 0) {
// genrand_int31 in mt19937ar.c performs a right shift
RETURN_LONG(php_mt_rand() >> 1);
}
...
}
PHPAPI uint32_t php_mt_rand(void)
{
/* Pull a 32-bit integer from the generator state
Every other access function simply transforms the numbers extracted here */
register uint32_t s1;
if (UNEXPECTED(!BG(mt_rand_is_seeded))) {
php_mt_srand(GENERATE_SEED());
}
if (BG(left) == 0) {
php_mt_reload();
}
--BG(left);
s1 = *BG(next)++; // PICKS NEXT SCRAMBLED STATE VALUE
s1 ^= (s1 >> 11);
s1 ^= (s1 << 7) & 0x9d2c5680U;
s1 ^= (s1 << 15) & 0xefc60000U;
return ( s1 ^ (s1 >> 18) );
}
s1表示置乱的状态值。在php_mt_rand()应用了4个操作之后,mt_rand()将它向右移动一位。显然,最后这个操作是不能逆转的。其他四个可以。
我们最终得到以下代码来撤销这些转换:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19def undo_php_mt_rand(s1):
"""Retrieves the merged state value from the value sent to the user.
"""
s1 ^= (s1 >> 18)
s1 ^= (s1 << 15) & 0xefc60000
s1 = undo_lshift_xor_mask(s1, 7, 0x9d2c5680)
s1 ^= s1 >> 11
s1 ^= s1 >> 22
return s1
def undo_lshift_xor_mask(v, shift, mask):
"""r s.t. v = r ^ ((r << shift) & mask)
"""
for i in range(shift, 32, shift):
v ^= (bits(v, i - shift, shift) & bits(mask, i, shift)) << i
return v
给定一个mt_rand()函数的输出,并猜测它的LSB,我们可以得到两个可能的置乱状态值:一个输出的LSB是0,另一个LSB是1。(有疑问有疑问)
将他们组合起来
让我们把这些逆向的步骤放在一起:
从mt_rand()中获取两个值,中间由226个其他值分隔:R000和R227;i, R000之前生成的值的数量。
从这些值中获取打乱的状态。
XOR那些状态并推断出初始状态228
从s228回到s0得到种子
1 | def main(_R000, _R227, offset): |
因为我们缺少R000和R227的LSB,所以我们需要尝试每种情况的算法。通常,这四种组合中只有一种会产生种子,而其他的组合是不可能产生种子的。
输出: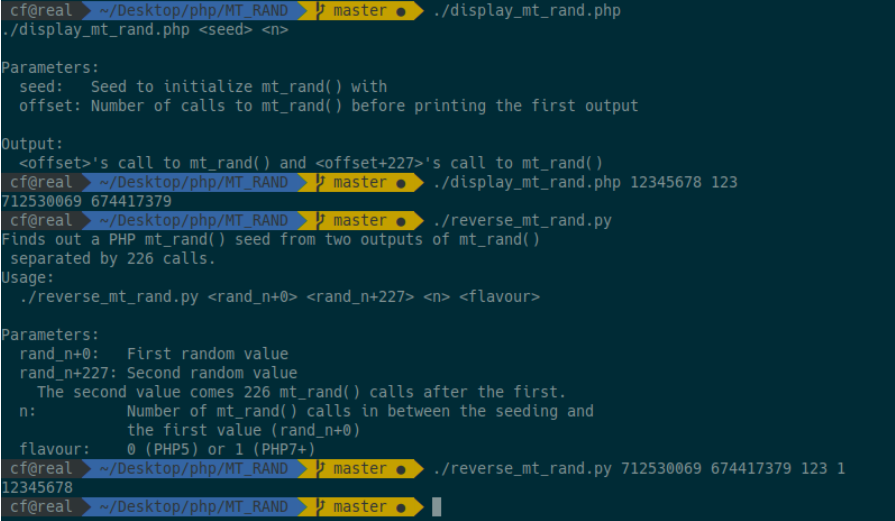
完整的python代码可以在我们的GitHub上找到。
结论
我们证明了,给定两个mt_rand()输出值被226个其他值分隔,可以在不使用任何暴力破解的情况下计算原始种子,从而获得任何以前或以后的mt_rand()的输出,从而有效地破坏mt_rand的PRNG算法。
hgame 二发入魂
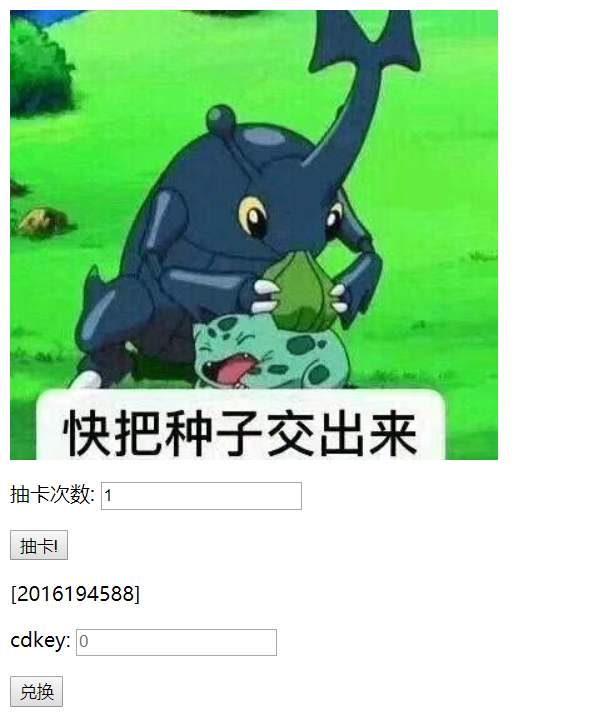
抽卡x次即生成x个随机数,再加上上面表情包的提示,判断题目应该是想让做题的人在cdkey处提交随机数种子,根据弹窗提示,需要在两秒内完成,最好写脚本完成(手速快点应该也行)
exp:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16import requests
import os
url = r"https://twoshot.hgame.n3ko.co/random.php?times=228"
session = requests.session()
response = session.get(url)
# print(response.text)
list = response.text.replace('[','').replace(']','').split(',')
# print(list)
cmd =os.popen("python reverse_mt_rand.py "+list[0]+" "+list[227]+" 0 0")
seed = cmd.read().strip()
print(seed)
cmd.close()
urlv = r"https://twoshot.hgame.n3ko.co/verify.php"
response2 = session.post(urlv,data={'ans':seed})
print(response2.text)