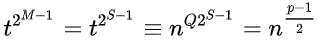task.py1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18from Crypto.Util.number import *
import gmpy2
from flag import flag
p = getPrime(256)
q = getPrime(256)
r = getPrime(512)
e = 2
m = bytes_to_long(flag)
n = p * q + r
c = pow(m, e, n)
with open('task', 'w') as f:
f.write("c = {}\n".format(str(c)))
f.write("e = {}\n".format(str(e)))
f.write("q = {}\n".format(str(q)))
f.write("n = {}\n".format(str(n)))
虽然有pow但不是RSA,因为n是素数
我觉得判断的原因就是p * q为非素数,再加上一个素数,就得到素数
后面知道是利用Tonelli–Shanks算法求解二次剩余问题。
已知n、c求m
参考:https://en.wikipedia.org/wiki/Tonelli%E2%80%93Shanks_algorithm
https://blog.csdn.net/wmdcstdio/article/details/49862189?locationNum=15
Tonelli–Shanks算法
Tonellii - Shanks算法(Shanks称为RESSOL算法)在模运算中用于求解的一个全等,其中p是质数:即求n模p的平方根。
Tonelli–Shanks不可用于复合模:求平方根模的复合数是一个与大整数分解等价的计算问题。
核心
给予一个非零n和一个奇素数p,欧拉判别法告诉我们n有一个平方根(例如,n是一个二次剩余)那么有:
相反,如果一个数z没有平方根(不满足二次剩余),则有:
我们不难发现z,因为在1和p-1之间的接近一半的的整数有这种性质,所以我们假定我们有这样的非二次剩余。
通过(通常情况下)重复除以2,我们可以把p-1写作$Q2^S$,而且此处Q为奇数,注意到如果我们尝试
接着
如果
那么R是n的一个平方根。否则对于M=S,我们有R和t满足
$R^2\equiv nt(mod\ p)$;和
t是一个1的$2^{M-1}$根(因为)
关键就是这里,如果满足此时t=1,那么R就是需要求解的r
如果我给一个R和t对于特定的M满足先前提到的(R不是n的平方根),我们能简单地计算出另外的R和t,且对于M-1满足先前提到的关系,这样我们能重复这一过程知道t变成1的2的$2^0$次方根,例如,t=1,在这时R是一个n的一个平方根。
我们可以检查t是否是1的一个$2^{M-2}$根通过开{M-1}次方,和检查是否等于1。如果是,那我们不需要做任何事,相同的R和t就可以了。但如果不是,${\displaystyle t^{2^{M-2}}}$一定要是-1(因为将它开方得到1,1模p只能有两个平方根1和-1)
为了找到一对新的R和t,我们能把R乘一个待定的因数b。接下来t一定要被因数$b^2$为了保证$R^2\equiv nt(mod\ p)$, 所以我们需要去找到一个因数$b^2$,以达成$tb^2$是一个1的$2^{M-2}$根,或者相同地,$b^2$是一个-1的$2^{M-2}$根。
关键的就是利用$z$,这个已知的非二次剩余数,欧拉判别法应用如上所示,${z^{Q}}$是-1的${2^{S-1}}$根,通过重复对${z^{Q}}$开方,我们可以得到一个$-1的2^i$次方根的序列。我们可以选择一个合适的去作为b,通过一点点变量维护和琐碎的情况压缩(翻不动),算法就有了。
例子
求解这样的全等式:
41是一个所需要的素数,并且 5是一个通过欧拉判别法得知的二次剩余数:$5^{\frac{41-1}{2}}=5^{20}=1$(正如之前,在${\displaystyle (\mathbb {Z} /41\mathbb {Z} )^{\times }}$ (41模整数的乘法群)被暗中$mod\ 41$)
类似的等于关系下面会多次出现,因为其实还隐藏了mod41
1.$p-1=40=5*2^3$,所以$Q \leftarrow\ 5$ , $S \leftarrow\ 3$
2.找到z
- $2{\frac{41-1}{2}}=1$,所以2是一个二次剩余数
- $3{\frac{41-1}{2}}=40=-1$,所以3是一个二次非剩余数,令$z \leftarrow\ 3$
3.令
- $M \leftarrow\ S=3$
- $c \leftarrow\ z^Q=3^5=38$
- $t \leftarrow\ n^Q=5^5=9$
- $R \leftarrow\ n^{\frac{Q+1}{2}}=5^{\frac{5+1}{2}}=2$
4.循环
- 第一次迭代:
- $t \neq\ 1$,所以我们没完成
- ${\displaystyle t^{2^{1}}=40}, {\displaystyle t^{2^{2}}=1} 所以 {\displaystyle i\leftarrow 2}$
- ${\displaystyle b\leftarrow c^{2^{M-i-1}}=38^{2^{3-2-1}}=38}$
- ${\displaystyle M\leftarrow i=2}$
- ${\displaystyle c\leftarrow b^{2}=38^{2}=9}$
- ${\displaystyle t\leftarrow tb^{2}=9\cdot 9=40}$
- ${\displaystyle R\leftarrow Rb=2\cdot 38=35}$
/n
- 二次迭代:
- ${\displaystyle t\neq 1}$, 所以我们还未完成
- ${\displaystyle t^{2^{1}}=1}$所以 ${\displaystyle i\leftarrow 1}$
- ${\displaystyle b\leftarrow c^{2^{M-i-1}}=9^{2^{2-1-1}}=9}$
- ${\displaystyle M\leftarrow i=1}$
- ${\displaystyle c\leftarrow b^{2}=9^{2}=40}$
- ${\displaystyle t\leftarrow tb^{2}=40\cdot 40=1}$
- ${\displaystyle R\leftarrow Rb=35\cdot 9=28}$
/n
三次迭代
- $t=1$,我们完成了,返回值$r=R=28$
的确,$28^2\equiv 5(mod\ 41)和(-28)^2\equiv13^2\equiv5(mod\ 41)$,所以这个算法最终产生了两个同余解
脚本
1 | from Crypto.Util.number import * |