2019高校运维挑战赛 WP-Crypto （未完）

Crypto

Word count: 3kReading time: 15 min

 2020/03/30   Share

rsa1

rsa.py

from flag import FLAG
from Crypto.Util.number import *
import gmpy2
import random

while True:
    p = int(gmpy2.next_prime(random.randint(10**399, 10**400-1)))
    q = int(str(p)[200:]+str(p)[:200])
    if gmpy2.is_prime(q):
        break

m = bytes_to_long(FLAG)
n = p*q
e = 65537
c = pow(m,e,n)

with open("enc","wb") as f:
    f.write(str(c))
    f.write("\n")
    f.write(str(n))

enc

1
2

16396023285324039009558195962852040868243807971027796599580351414803675753933120024077886501736987010658812435904022750269541456641256887079780585729054681025921699044139927086676479128232499416835051090240458236280851063589059069181638802191717911599940897797235038838827322737207584188123709413077535201099325099110746196702421778588988049442604655243604852727791349351291721230577933794627015369213339150586418524473465234375420448340981330049205933291705601563283196409846408465061438001010141891397738066420524119638524908958331406698679544896351376594583883601612086738834989175070317781690217164773657939589691476539613343289431727103692899002758373929815089904574190511978680084831183328681104467553713888762965976896013404518316128288520016934828176674482545660323358594211794461624622116836
21173064304574950843737446409192091844410858354407853391518219828585809575546480463980354529412530785625473800210661276075473243912578032636845746866907991400822100939309254988798139819074875464612813385347487571449985243023886473371811269444618192595245380064162413031254981146354667983890607067651694310528489568882179752700069248266341927980053359911075295668342299406306747805925686573419756406095039162847475158920069325898899318222396609393685237607183668014820188522330005608037386873926432131081161531088656666402464062741934007562757339219055643198715643442608910351994872740343566582808831066736088527333762011263273533065540484105964087424030617602336598479611569611018708530024591023015267812545697478378348866840434551477126856261767535209092047810194387033643274333303926423370062572301

参考：Ashen师兄的比赛wp，以及https://github.com/7feilee/ctf_writeup/tree/master/2019/%E9%AB%98%E6%A0%A1%E7%BD%91%E7%BB%9C%E4%BF%A1%E6%81%AF%E5%AE%89%E5%85%A8%E7%AE%A1%E7%90%86%E8%BF%90%E7%BB%B4%E6%8C%91%E6%88%98%E8%B5%9B_2019

方法一

参考Ashen

1 2	p = int(gmpy2.next_prime(random.randint(10399, 10400-1))) q = int(str(p)[200:]+str(p)[:200])

p q为质数，400位，q为p的高200位和低200位互换
令p = a(10**200)+b；q = b(10**200)+a （a和b分别为200位）

$n = p\times q$ $n = [a\times(10^{200})+b]\times [b\times(10^{200})+a]$

展开得到

$n=ab\times10^{400}+10^{200}(a^2+b^2)+ab \ （1）$

接下来就是数学认识吧，n的数值是和ab有关的，可以知道两个200位的整数相乘，最多为400位，也就是(1)式中最后一项和n的最后若干位有关，而且最多400位；而第一项和n的前若干位有关，而且至多400位，若是没有中间那项，我们就可以直接提取ab了，但是这是在扯蛋，有了中间那一项其实方便了我们提取ab，我们知道中间那一项影响了n的中间位，而且同样最多400位，也就是：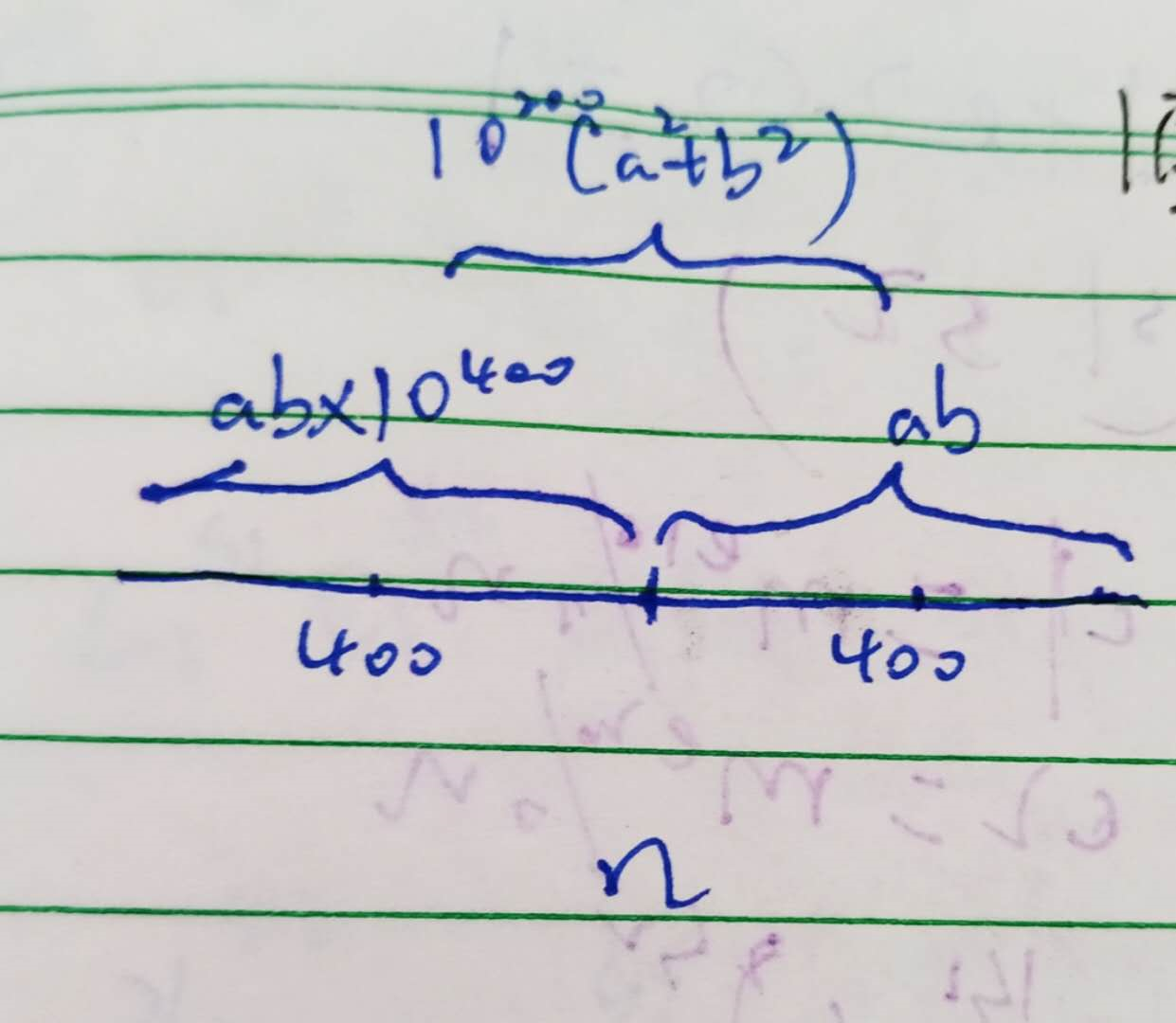

所以如果我们想要构造ab项，我们可以提取出n的最后200位，因为要保证不和中间的部分产生进位关系。
但是前200位不能直接提取，因为中间部分可能产生了进位，而我们知道前若干位是没有进位的，产生进位的只有后几位，所以

1	ab = int(str(n)[:197]+str(i)+str(n)[-200:])

爆破可能产生进位的那几项

import gmpy2
import libnum
e = 65537
c = 16396023285324039009558195962852040868243807971027796599580351414803675753933120024077886501736987010658812435904022750269541456641256887079780585729054681025921699044139927086676479128232499416835051090240458236280851063589059069181638802191717911599940897797235038838827322737207584188123709413077535201099325099110746196702421778588988049442604655243604852727791349351291721230577933794627015369213339150586418524473465234375420448340981330049205933291705601563283196409846408465061438001010141891397738066420524119638524908958331406698679544896351376594583883601612086738834989175070317781690217164773657939589691476539613343289431727103692899002758373929815089904574190511978680084831183328681104467553713888762965976896013404518316128288520016934828176674482545660323358594211794461624622116836
n = 21173064304574950843737446409192091844410858354407853391518219828585809575546480463980354529412530785625473800210661276075473243912578032636845746866907991400822100939309254988798139819074875464612813385347487571449985243023886473371811269444618192595245380064162413031254981146354667983890607067651694310528489568882179752700069248266341927980053359911075295668342299406306747805925686573419756406095039162847475158920069325898899318222396609393685237607183668014820188522330005608037386873926432131081161531088656666402464062741934007562757339219055643198715643442608910351994872740343566582808831066736088527333762011263273533065540484105964087424030617602336598479611569611018708530024591023015267812545697478378348866840434551477126856261767535209092047810194387033643274333303926423370062572301
for i in range(1000):
    print ("i=",i)
    ab = int(str(n)[:197]+str(i)+str(n)[-200:])
    print ("ab=",ab)
    print (n-ab*(10**400)-ab)
    a2pb2 = (n-ab*(10**400)-ab)//(10**200) #求出a^2+b^2
    if a2pb2 < 0:
        continue
    apb = gmpy2.isqrt(a2pb2+2*ab) #求出a+b
    if apb**2 - a2pb2-2*ab == 0:
        print ("found ab")
        break
phi = n-(apb*10**200+apb)+1
d = gmpy2.invert(e, phi)
flag = pow(c,d,n)
print (libnum.n2s(flag))
#flag{637c3dda0a943c9e837ede64cba71cbcf8e0be7bb1ca9ea1de8b9aa589ce703f}

但其实再怎么进位也不可能影响这么多位的，所以我觉得不用range（1000），range（10）就可以了

import gmpy2
import libnum
e = 65537
c = 16396023285324039009558195962852040868243807971027796599580351414803675753933120024077886501736987010658812435904022750269541456641256887079780585729054681025921699044139927086676479128232499416835051090240458236280851063589059069181638802191717911599940897797235038838827322737207584188123709413077535201099325099110746196702421778588988049442604655243604852727791349351291721230577933794627015369213339150586418524473465234375420448340981330049205933291705601563283196409846408465061438001010141891397738066420524119638524908958331406698679544896351376594583883601612086738834989175070317781690217164773657939589691476539613343289431727103692899002758373929815089904574190511978680084831183328681104467553713888762965976896013404518316128288520016934828176674482545660323358594211794461624622116836
n = 21173064304574950843737446409192091844410858354407853391518219828585809575546480463980354529412530785625473800210661276075473243912578032636845746866907991400822100939309254988798139819074875464612813385347487571449985243023886473371811269444618192595245380064162413031254981146354667983890607067651694310528489568882179752700069248266341927980053359911075295668342299406306747805925686573419756406095039162847475158920069325898899318222396609393685237607183668014820188522330005608037386873926432131081161531088656666402464062741934007562757339219055643198715643442608910351994872740343566582808831066736088527333762011263273533065540484105964087424030617602336598479611569611018708530024591023015267812545697478378348866840434551477126856261767535209092047810194387033643274333303926423370062572301
for i in range(10):
    print ("i=",i)
    ab = int(str(n)[:199]+str(i)+str(n)[-200:])
    print ("ab=",ab)
    print (n-ab*(10**400)-ab)
    a2pb2 = (n-ab*(10**400)-ab)//(10**200)
    if a2pb2 < 0:
        continue
    apb = gmpy2.isqrt(a2pb2+2*ab)
    if apb**2 - a2pb2-2*ab == 0:
        print ("found ab")
        break
phi = n-(apb*10**200+apb)+1
d = gmpy2.invert(e, phi)
flag = pow(c,d,n)
print (libnum.n2s(flag))

0.3s出结果，虽然师兄那个脚本也很快出（0.5s）

方法二

说是双变量的Coppersmith’s求解

def coron(pol, X, Y, k=2, debug=False):
    """
    Returns all small roots of pol. 
    Applies Coron's reformulation of Coppersmith's algorithm for finding small
    integer roots of bivariate polynomials modulo an integer.  # 求二元多项式的小整数根。
    Args:
        pol: The polynomial to find small integer roots of.
        X: Upper limit on x. # x的上限
        Y: Upper limit on y. # y的上限
        k: Determines size of lattice. Increase if the algorithm fails.
        debug: Turn on for debug print stuff.
    Returns:
        A list of successfully found roots [(x0,y0), ...].
    Raises:
        ValueError: If pol is not bivariate
    """

    if pol.nvariables() != 2:
        raise ValueError("pol is not bivariate")

    P.<x,y> = PolynomialRing(ZZ)
    pol = pol(x,y)

    # Handle case where pol(0,0) == 0
    xoffset = 0

    while pol(xoffset,0) == 0:
        xoffset += 1

    pol = pol(x+xoffset,y)

    # Handle case where gcd(pol(0,0),X*Y) != 1
    while gcd(pol(0,0), X) != 1:
        X = next_prime(X, proof=False)

    while gcd(pol(0,0), Y) != 1:
        Y = next_prime(Y, proof=False)

    pol = P(pol/gcd(pol.coefficients())) # seems to be helpful
    p00 = pol(0,0)
    delta = max(pol.degree(x),pol.degree(y)) # maximum degree of any variable

    W = max(abs(i) for i in pol(x*X,y*Y).coefficients())
    u = W + ((1-W) % abs(p00))
    N = u*(X*Y)^k # modulus for polynomials

    # Construct polynomials
    p00inv = inverse_mod(p00,N)
    polq = P(sum((i*p00inv % N)*j for i,j in zip(pol.coefficients(),
                                                 pol.monomials())))
    polynomials = []
    for i in range(delta+k+1):
        for j in range(delta+k+1):
            if 0 <= i <= k and 0 <= j <= k:
                polynomials.append(polq * x^i * y^j * X^(k-i) * Y^(k-j))
            else:
                polynomials.append(x^i * y^j * N)

    # Make list of monomials for matrix indices
    monomials = []
    for i in polynomials:
        for j in i.monomials():
            if j not in monomials:
                monomials.append(j)
    monomials.sort()

    # Construct lattice spanned by polynomials with xX and yY
    L = matrix(ZZ,len(monomials))
    for i in range(len(monomials)):
        for j in range(len(monomials)):
            L[i,j] = polynomials[i](X*x,Y*y).monomial_coefficient(monomials[j])

    # makes lattice upper triangular
    # probably not needed, but it makes debug output pretty
    L = matrix(ZZ,sorted(L,reverse=True))

    if debug:
        print("Bitlengths of matrix elements (before reduction):")
        print(L.apply_map(lambda x: x.nbits()).str())

    L = L.LLL()

    if debug:
        print("Bitlengths of matrix elements (after reduction):")
        print(L.apply_map(lambda x: x.nbits()).str())

    roots = []

    for i in range(L.nrows()):
        if debug:
            print("Trying row %d" % i)

        # i'th row converted to polynomial dividing out X and Y
        pol2 = P(sum(map(mul, zip(L[i],monomials)))(x/X,y/Y))

        r = pol.resultant(pol2, y)

        if r.is_constant(): # not independent
            continue

        for x0, _ in r.univariate_polynomial().roots():
            if x0-xoffset in [i[0] for i in roots]:
                continue
            if debug:
                print("Potential x0:",x0)
            for y0, _ in pol(x0,y).univariate_polynomial().roots():
                if debug:
                    print("Potential y0:",y0)
                if (x0-xoffset,y0) not in roots and pol(x0,y0) == 0:
                    roots.append((x0-xoffset,y0))
    return roots
n = 21173064304574950843737446409192091844410858354407853391518219828585809575546480463980354529412530785625473800210661276075473243912578032636845746866907991400822100939309254988798139819074875464612813385347487571449985243023886473371811269444618192595245380064162413031254981146354667983890607067651694310528489568882179752700069248266341927980053359911075295668342299406306747805925686573419756406095039162847475158920069325898899318222396609393685237607183668014820188522330005608037386873926432131081161531088656666402464062741934007562757339219055643198715643442608910351994872740343566582808831066736088527333762011263273533065540484105964087424030617602336598479611569611018708530024591023015267812545697478378348866840434551477126856261767535209092047810194387033643274333303926423370062572301
#ZZ = Zmod(n)
c = 16396023285324039009558195962852040868243807971027796599580351414803675753933120024077886501736987010658812435904022750269541456641256887079780585729054681025921699044139927086676479128232499416835051090240458236280851063589059069181638802191717911599940897797235038838827322737207584188123709413077535201099325099110746196702421778588988049442604655243604852727791349351291721230577933794627015369213339150586418524473465234375420448340981330049205933291705601563283196409846408465061438001010141891397738066420524119638524908958331406698679544896351376594583883601612086738834989175070317781690217164773657939589691476539613343289431727103692899002758373929815089904574190511978680084831183328681104467553713888762965976896013404518316128288520016934828176674482545660323358594211794461624622116836
def test():
    P.<x,y> = PolynomialRing(ZZ)
    pol = (10^200*x+y)*(10^200*y+x) - n # Should have a root at (x0,y0)
    XX = next_prime(10^200)
    YY = next_prime(10^200)
    kk = 1
    root = coron(pol, XX, YY, k=2, debug=1)
    print (root)
    for i in root:
        print("aaa")
        e = 65537
        x0_2, y0_2 = 80554375634577518615438386695008921410006481979463250396364716867580983517518170157390631558754951379984609818401525153158058049179857450828511300732679873231618529488409644674348216778296766615218923,26284188956566787061488395375038990922315226573136209037057271138009190100783239284290331572584174262962398525057079432276956326316964537561436371572902729190352463910337199538520792220209028051162087
        p = 10^200*y0_2+x0_2
        q = 10^200*x0_2+y0_2
        phi = (p-1)*(q-1)
        print(n)
        print(p*q ==n)
        d = inverse_mod(e, phi)
        print (pow(c,d,n))
        #print(long_to_bytes(pow(c,d,n)))
        return
test()
print("done!!!")

from Crypto.Util.number import *
m=1509929362729717043022300489487994782016787576071736289063415995952567583629223176951694138781885206841482303701909036288710954561973833150311071565711672911612886607485
print (long_to_bytes(m))
#b'flag{637c3dda0a943c9e837ede64cba71cbcf8e0be7bb1ca9ea1de8b9aa589ce703f}'

套用的是https://github.com/ubuntor/coppersmith-algorithm/blob/master/coppersmith.sage 的脚本，原脚本有两个例程，第一个是恢复p、q，在给了n和p的低位的值；第二个是恢复p、q，在给了n和p的高位的值。

def main():
    # Example 1: recover p,q prime given n=pq and the lower bits of p

    print "---EXAMPLE 1---"

    nbits = 512 # bitlength of primes
    p = random_prime(2^nbits-1, proof=False, lbound=2^(nbits-1))
    q = random_prime(2^nbits-1, proof=False, lbound=2^(nbits-1))
    n = p*q

    lbits = 300 
    ln = 2^lbits
    p0 = p % ln # number of lower bits of p   模运算可以得到p的低位（二进制）

    x0 = p // ln # upper bits of p   整除可以得到p的高位（二进制）
    y0 = q // ln # upper bits of q   整除可以得到q的高位（二进制）

    #print 'p =',p
    #print 'q =',q
    #print 'x0 =',x0
    #print 'y0 =',y0

    print 'Given:'
    print 'n =',n
    print 'p0 =',p0

    # Recovery starts here
    q0 = (n * inverse_mod(p0,ln)) % ln     虽然不知道为什么 但是就是得到q的低位
    assert q0 == q % ln
    X = Y = 2^(nbits+1-lbits) # bounds on x0 and y0

    P.<x,y> = PolynomialRing(ZZ)
    pol = (ln*x+p0)*(ln*y+q0) - n # Should have a root at (x0,y0)

    x0_2, y0_2 = coron(pol, X, Y, k=2, debug=True)[0]
    p_2 = x0_2*ln + p0
    q_2 = y0_2*ln + q0

    print
    print 'Recovered:'
    print 'x0 =',x0_2
    print 'y0 =',y0_2
    print 'p =',p_2
    print 'q =',q_2

    # Example 2: recover p,q prime given n=pq and the upper bits of p
    # This can be done with a univariate polynomial and Howgrave-Graham,
    # but this is another way to do it with a bivariate polynomial.

    print "---EXAMPLE 2---"

    nbits = 512 # bitlength of primes
    p = random_prime(2^nbits-1, proof=False, lbound=2^(nbits-1))
    q = random_prime(2^nbits-1, proof=False, lbound=2^(nbits-1))
    n = p*q

    lbits = (512-300) # number of masked bits of p 
    ln = 2^lbits
    p0 = p // ln

    x0 = p % ln # lower bits of p
    y0 = q % ln # lower bits of q

    #print 'p =',p
    #print 'q =',q

    print 'Given:'
    print 'n =',n
    print 'p0 =',p0

    # Recovery starts here
    q0 = floor(n / (p0*ln))//ln
    X = Y = 2^(lbits+2) # bounds on x0 and y0
    P.<x,y> = PolynomialRing(ZZ)
    # Should have a root at (x0,y0) +/- some bits of q0
    pol = (x+p0*ln)*(y+q0*ln) - n

    x0_2, y0_2 = coron(pol, X, Y, k=2, debug=True)[0]
    p_2 = p0*ln + x0_2
    q_2 = q0*ln + y0_2

    print
    print 'Recovered:'
    print 'x0 =',x0_2
    print 'y0 =',y0_2
    print 'p =',p_2
    print 'q =',q_2

if __name__ == '__main__':
    main()

里面还有三变量的求解脚本，值得备注一下

算法没有去了解，目前对我来说实在是难以下咽…

本机没有sage，可以到：https://sagecell.sagemath.org/ 运行第一段代码，但是网站没有Crypto库，连n2s也用不了…所以先求出m的整数形式，再转成字符串

使用这个脚本，大概是需要能将p和q带换成x和y的表达式，然后x和y又要有位数上的联系

rsa2

参考：http://soreatu.com/ctf/writeups/Writeup%20for%20EIS%202019.html

from flag import FLAG
from Crypto.Util.number import *
import os
import gmpy2

p = getPrime(2048)
q = gmpy2.next_prime(bytes_to_long(os.urandom(32)*8))
n = p*q
e = 65537

m = bytes_to_long(FLAG)
enc = pow(m,e,n)

with open("enc","wb") as f:
    f.write(str(enc)+"\n")
    f.write(str(n)+"\n")

显然就是要从q入手，因为构造起来有猫腻
如果我们令x = os.urandom(32)，那么q实际上等于x + (x<<256) + (x<<512) + … + （x<<1792) + b，其中b就是由next_prime产生的一个很小的正数。
根据素数定理，b大概在ln(2**2048) = 1420左右。

素数定理：

定义 $π(x)$ 为素数计数函数，也就是小于等于$x$ 的素数个数。例如 $π(10)=4$，因为共有 4 个素数小于等于 10，分别是 2、3、5、7。素数定理的叙述为：当 $x$ 趋近无限，$π(x)$ 和 ${\displaystyle {\frac {x}{\ln x}}}$ 的比值趋近 1。其数学式写做
${\displaystyle \lim {x\to \infty }{\frac {\;\pi (x)\;}{\frac {x}{\ln(x)}}}=1}$
浅白的说，当 x 很大的时候，$π(x)$ 差不多等于 ${\displaystyle {\frac {x}{\ln x}}}$。该定理被认为是素数的渐进分布定律，以渐进符号可简化为
${\displaystyle \pi (x)\sim {\frac {x}{\ln x}}}$。
注意到，上式并不是说指随着$ x $趋近无限，${\displaystyle \pi (x)}$ 与 ${\displaystyle {\frac {x}{\ln x}}}$的差趋近于 0。而是随着 $x $趋近无限，${\displaystyle \pi (x)}$与 ${\displaystyle {\frac {x}{\ln x}}}$的相对误差趋近于 0。
素数定理有一个等价数是关于第 n 个素数${\displaystyle p{n}}$的渐近估计式
${\displaystyle p_{n}\sim n\ln \,n}$

关于怎么得知b大概在ln(2**2048) = 1420还有待思考
我觉得知不知道b大约的值问题不大

sage脚本1:

n = 120807710153113702551615579080626349972702435654213602643278178850601270671946229285821528380336690426317604059622034599839001416930715968066016772516322170847232613450387418879151680919583407733398280475244970196660246303755390654445483988806163997943960045202300170321033632884706732013873256539789027552900587666422370948750842536533923935656875965991272731558533581897633592458155859972323709278905289729445241014357315813048740496355157322217479024997808766708783034169626351658483634985294355975778256304622956911622334081421352132051371869608818591717661111189285407351900021893457439899221542567630909004930602528901255429064258255953091799356807896508016798627878778491866567622281528441807056062152648122769596905617532839645811871242955534491003544450002957748265702306031022676181061669831693628120952508570252446308607118097142440911574131249381253267168309302968966178203572103064042325655007707720847432033652545364390235670894288288369956445797446648862192044259720010703057599068467348014822871417162946598110099990800849922664801383108437169282005803013729663209291895365964487113632471631243676196750054390014101920098216264290734689252677221687512705895162185620154778448467145374612676883160397044672382343419867

# calculating s
s = 0
for i in range(8):
    s += 1 << (i*256)


kbits = 256

PR.<x> = PolynomialRing(Zmod(n))

for i in range(1, 3000):
    try:
        print(i)
        f = x*s + i
        f = f.monic() # Must first turn into monic polynomial.
        x0 = f.small_roots(X=2^kbits, beta=0.4)[0]
        
        print ("x: %s" %hex(int(x0)))
        
    except:
        continue

算的挺慢，之后求得x（当i=1452），根据q = s*x + b可以算出q，成功分解n。
（但是我在网上的sage跑到478就卡住了）

接下来就是正常的解密：

from Crypto.Util.number import *

n = 120807710153113702551615579080626349972702435654213602643278178850601270671946229285821528380336690426317604059622034599839001416930715968066016772516322170847232613450387418879151680919583407733398280475244970196660246303755390654445483988806163997943960045202300170321033632884706732013873256539789027552900587666422370948750842536533923935656875965991272731558533581897633592458155859972323709278905289729445241014357315813048740496355157322217479024997808766708783034169626351658483634985294355975778256304622956911622334081421352132051371869608818591717661111189285407351900021893457439899221542567630909004930602528901255429064258255953091799356807896508016798627878778491866567622281528441807056062152648122769596905617532839645811871242955534491003544450002957748265702306031022676181061669831693628120952508570252446308607118097142440911574131249381253267168309302968966178203572103064042325655007707720847432033652545364390235670894288288369956445797446648862192044259720010703057599068467348014822871417162946598110099990800849922664801383108437169282005803013729663209291895365964487113632471631243676196750054390014101920098216264290734689252677221687512705895162185620154778448467145374612676883160397044672382343419867
c = 72074917741352632160674674423757226112732503986000125039486711125930276990656443924045288819165868627345704261550380026428346484029915532163917560135274130060403712677039409151760010987858845886090016665156558016254326826349547059132398165597146069935545654906860020446697981554235605548000668071179792369940040506180386344236709376665259555250931229064902253547279742091220081637632484839561818114867753305491466827132794867249268560394596282075249284471959669850300827075751375695495341046098821675671765630616585051408145283934310355450905091174225551852913024234768486683298136180488046648783548871491321003078465957075420450585181898780566907562110082339288183440201802995310694770151937718551875438109333769631500406936973469725930357855181743773516614272920932620803689778201192376634531897671943274986227782204268656867015692338457851232257902297364385868885931304585042560760186518312999852311004441119468693156565576967918680895591024375643850476541598453775623072668482295311781424458452933753379256069914551757794501890946111771992773535292266796984300649540507830481957270227762148818664162360269195888312995110145796745786950401203936544098266440768709581819476569480672433242587899101968249584078375546230742964233750
e = 65537

b = 1452
x = 0x377c84c8a5d8796d45f4736bfdeb638fe56b732d151a5a0ae317c3e4bf88c28b

s = 0
for i in range(8):
    s += 1 << (i*256)

p = x*s + b
# p = 7004509226017637089988705520937631339897192947483065164943452309041913623129146263923174422404097665004135635478475556696377225841003919854716749299322196806963356447396854333399946296722120278944449732965634423393409679543683846502213180200860496072514760412108169662614749296168127807006670959727343682333756381711955847248499610590647032124815312578729035756164588000435826272348172873765119706049026161200076229607613023276462703666278152053357550784368621764632121070911804535678091316200064926136006296281350497851425130626427731687110200771361941797756340109574629221793536665232298530087134136937005321865271
q = n // p
assert p*q == n

d = inverse(e, (p-1)*(q-1))
m = pow(c, d, n)
print(long_to_bytes(m))
# b'flag{60ea503347a3cdd3181644d07599b7acf97f8382e0376061dc4902776046d43b}'

参考https://github.com/7feilee/ctf_writeup/tree/master/2019/%E9%AB%98%E6%A0%A1%E7%BD%91%E7%BB%9C%E4%BF%A1%E6%81%AF%E5%AE%89%E5%85%A8%E7%AE%A1%E7%90%86%E8%BF%90%E7%BB%B4%E6%8C%91%E6%88%98%E8%B5%9B_2019#Signature

p 256 bit重复多次，构造LLL求解

sage脚本2：

e = 65537
c = 72074917741352632160674674423757226112732503986000125039486711125930276990656443924045288819165868627345704261550380026428346484029915532163917560135274130060403712677039409151760010987858845886090016665156558016254326826349547059132398165597146069935545654906860020446697981554235605548000668071179792369940040506180386344236709376665259555250931229064902253547279742091220081637632484839561818114867753305491466827132794867249268560394596282075249284471959669850300827075751375695495341046098821675671765630616585051408145283934310355450905091174225551852913024234768486683298136180488046648783548871491321003078465957075420450585181898780566907562110082339288183440201802995310694770151937718551875438109333769631500406936973469725930357855181743773516614272920932620803689778201192376634531897671943274986227782204268656867015692338457851232257902297364385868885931304585042560760186518312999852311004441119468693156565576967918680895591024375643850476541598453775623072668482295311781424458452933753379256069914551757794501890946111771992773535292266796984300649540507830481957270227762148818664162360269195888312995110145796745786950401203936544098266440768709581819476569480672433242587899101968249584078375546230742964233750
n = 120807710153113702551615579080626349972702435654213602643278178850601270671946229285821528380336690426317604059622034599839001416930715968066016772516322170847232613450387418879151680919583407733398280475244970196660246303755390654445483988806163997943960045202300170321033632884706732013873256539789027552900587666422370948750842536533923935656875965991272731558533581897633592458155859972323709278905289729445241014357315813048740496355157322217479024997808766708783034169626351658483634985294355975778256304622956911622334081421352132051371869608818591717661111189285407351900021893457439899221542567630909004930602528901255429064258255953091799356807896508016798627878778491866567622281528441807056062152648122769596905617532839645811871242955534491003544450002957748265702306031022676181061669831693628120952508570252446308607118097142440911574131249381253267168309302968966178203572103064042325655007707720847432033652545364390235670894288288369956445797446648862192044259720010703057599068467348014822871417162946598110099990800849922664801383108437169282005803013729663209291895365964487113632471631243676196750054390014101920098216264290734689252677221687512705895162185620154778448467145374612676883160397044672382343419867
pattern_size = 256
prime_size = 2048
x = 2**pattern_size
d0 = 2**pattern_size - 1
w = 2**prime_size
u, v = divmod(n, w)
M = matrix([[x, 0, u * d0 % w],
            [0, x, v * d0 % w],
            [0, 0,         w]])

for vec in M.LLL():
  bx, ax = vec[0], -vec[1]
  p = gcd(ax * w + bx, n)
  if 1 < p < n:
    q = n // p
    break

phi = (p-1)*(q-1)
d = inverse_mod(e, phi)
print (d)
print((pow(c, d, n)))
#print(long_to_bytes(pow(c, d, n)))
#flag{60ea503347a3cdd3181644d07599b7acf97f8382e0376061dc4902776046d43b}

无关信息
Wiener’s Attack
$N = pq \ \varphi(n) = (p-1)(q-1)=pq - (p + q) + 1=N - (p + q) + 1\ $$$$\because p,q非常大,\therefore pq\gg p+q ,\therefore\varphi(n)\approx N\ $$$$\because ed\equiv1 mod \varphi(n),\therefore ed-1=k\varphi(n),这个式子两边同除 dφ(n) 可得：$$$$\ \frac{e}{\varphi(n)}-\frac{k}{d}=\frac{1}{d\varphi(n)}\ $$$$\because \varphi(n)\approx N,\therefore \frac{e}{N}-\frac{k}{d}=\frac{1}{d\varphi(n)},同样 dφ(n) 是一个很大的数，所以 \frac{e}{N} 略大于\frac{k}{d}$

Author：DGZ

原文链接：https://dgz-cyber.github.io/2020/03/30/2019%E9%AB%98%E6%A0%A1%E8%BF%90%E7%BB%B4%E6%8C%91%E6%88%98%E8%B5%9B%20WP-Crypto%20%EF%BC%88%E6%9C%AA%E5%AE%8C%EF%BC%89/

发表日期：March 30th 2020, 10:45:56 pm

更新日期：May 4th 2020, 11:31:55 pm

Next Post

赵师傅b站视频学习记录以及一点misc (未完)
Previous Post

BJDCTF WP - WEB-1

CATALOG

1. rsa1
1. 1.1. 方法一
2. 1.2. 方法二
2. rsa2

