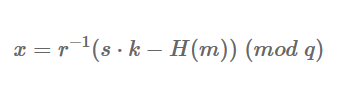DGZ's Blog.

安恒四月赛-Crypto

Crypto
Word count: 4.9kReading time: 27 min
2020/04/25 Share

难得两道题都会做

notrsa

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import getPrime as getprime ,long_to_bytes,bytes_to_long,inverse
from secret import flag,p,q
from sympy import isprime,nextprime
import random

m=bytes_to_long(flag)
n=p*q
g=n+1
r=random.randint(1,n)

c=(pow(g,m,n*n)*pow(r,n,n*n))%(n*n)

print "c=%d"%(c)
print "n=%d"%(n)
'''
c=29088911054711509252215615231015162998042579425917914434962376243477176757448053722602422672251758332052330100944900171067962180230120924963561223495629695702541446456981441239486190458125750543542379899722558637306740763104274377031599875275807723323394379557227060332005571272240560453811389162371812183549
n=6401013954612445818165507289870580041358569258817613282142852881965884799988941535910939664068503367303343695466899335792545332690862283029809823423608093
'''

我一开始在谷歌查到的是：http://blog.rb-tree.xyz/2020/03/09/zer0pts-ctf-2020-dirty-laundry/
原本想着这个应该是这道题的简化版
没想到是更简单的东西
里面提到Paillier cryptosystem 这一玩意
于是我百度了一下查到了：https://blog.csdn.net/qq_33885461/article/details/86555560
解密过程都写好了

简单记录：
3.1 秘钥生成

1.随机选择两个大质数p和q满足$gcd(pq,(p−1)(q−1)=1$。 这个属性是保证两个质数长度相等。
2.计算$ n=pq$，和$λ=lcm(p−1,q−1)$
3.选择随机整数$g(∈Z_{n^2}^∗​) $ 4.使得满足n整除g的阶。
5.定义 $L(x)=(x−1)/n$
6.计算$μ=(L(g^λmodn^2))^{−1}mod\ n$
7.公钥(n,g) 私钥为(λ,μ)

3.2 加密

1.m为原文(0≤m<n)
2.选择随机数$r(0<r<n,r∈Z_{n^2}^∗​)$ 且$gcd(r,n)=1$
3.加密$ c=g^m∗r^nmodn^2$

3.3 解密

首先看到n挺短的，拖进yafu分解得到p和q
因为这个是求lamda的关键
利用gmpy2.lcm可以求出lamda
sage可以直接用lcm
然后照着解密过程写脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import getPrime as getprime ,long_to_bytes,bytes_to_long,inverse
import random
import gmpy2
def L(x):
	n=6401013954612445818165507289870580041358569258817613282142852881965884799988941535910939664068503367303343695466899335792545332690862283029809823423608093
	k=(x-1)//n
	return k
n=6401013954612445818165507289870580041358569258817613282142852881965884799988941535910939664068503367303343695466899335792545332690862283029809823423608093
c=29088911054711509252215615231015162998042579425917914434962376243477176757448053722602422672251758332052330100944900171067962180230120924963561223495629695702541446456981441239486190458125750543542379899722558637306740763104274377031599875275807723323394379557227060332005571272240560453811389162371812183549
g=n+1
p=80006336965345725157774618059504992841841040207998249416678435780577798937819
q=80006336965345725157774618059504992841841040207998249416678435780577798937447
print (gmpy2.lcm(p-1,q-1)) #3200506977306222909082753644935290020679284629408806641071426440982942399994390761618504486309093909033612342740607826856064668096014463079124333912866414
lamda=3200506977306222909082753644935290020679284629408806641071426440982942399994390761618504486309093909033612342740607826856064668096014463079124333912866414
L_1=inverse(L(pow(g,lamda,n*n)),n*n)%n
miu=L_1%n
m=L(pow(c,lamda,n*n))*miu%n
print(long_to_bytes(m))
#b'flag{5785203dbe6e8fd8bdbab860f5718155}'

当然以上是快速解题的方法，如果想推导公式从而解题呢？

参考师傅：http://caoyi.site/?p=162

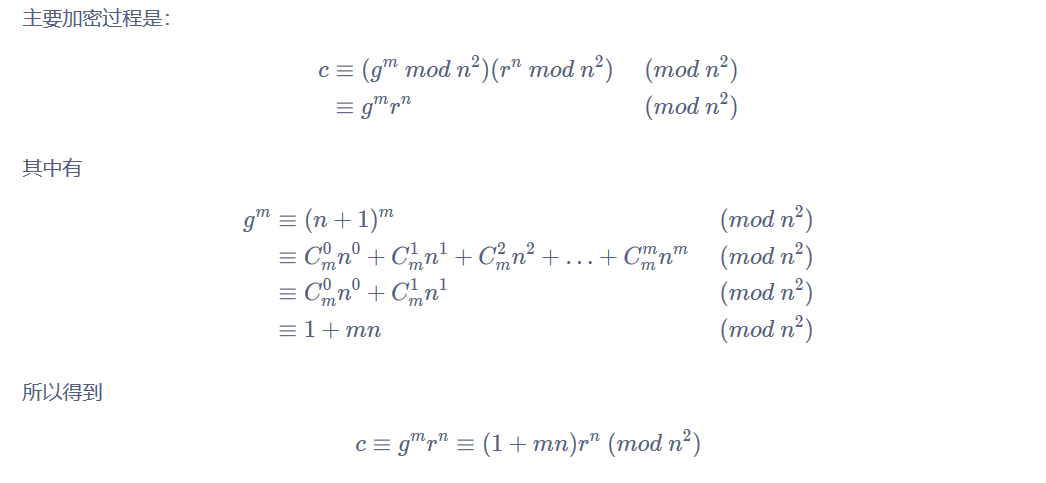
J7Wz3F.png

$g^m$这一项展开的真的是神仙，膜拜膜拜

之后现在就要想办法消除掉 $r^n$ 的影响，因为r不知道，而我们要求m

不难发现

一开始很疑惑，但是后面得到师傅的解释

所以接下来我们需要由$ r^n mod n$ 得到 $r$ 的值或者 $r^n mod n^2$的值，才可以对 $ r^n $ 在模 $n^2$ 下求逆元。这里可以将 $r^n mod n$ 分别对 $n$ 的两个因数 $p,q$取模，然后再用中国剩余定理（CRT）合起来，从而得到 $r$。

然后我们只需要计算$ r^n mod\ n^2 $ 的逆元并与$ c$ 相乘，就得到$ (1+mn) mod\ n^2$ ，也就得到了 $m$ 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#exp.py
from Crypto.Util.number import long_to_bytes, inverse
from functools import reduce

c = 29088911054711509252215615231015162998042579425917914434962376243477176757448053722602422672251758332052330100944900171067962180230120924963561223495629695702541446456981441239486190458125750543542379899722558637306740763104274377031599875275807723323394379557227060332005571272240560453811389162371812183549
n = 6401013954612445818165507289870580041358569258817613282142852881965884799988941535910939664068503367303343695466899335792545332690862283029809823423608093
p = 80006336965345725157774618059504992841841040207998249416678435780577798937819
q = 80006336965345725157774618059504992841841040207998249416678435780577798937447
g = n+1
phi = (p-1)*(q-1)
rn = c % n

x1 = rn % p
d1 = inverse(q, p-1)
r1 = pow(x1, d1, p)

x2 = rn % q
d2 = inverse(p, q-1)
r2 = pow(x2, d2, q)


def CRT(m, a):
    Num = len(m)
    M = reduce(lambda x, y: x*y, m)
    Mi = [M//i for i in m]
    t = [inverse(Mi[i], m[i]) for i in range(Num)]
    x = 0
    for i in range(Num):
        x += a[i]*t[i]*Mi[i]
    return x % M


r = CRT([p, q], [r1, r2])

R = pow(r, n, n*n)
R_inv = inverse(R, n*n)
mn = (c*R_inv) % (n*n)
m = (mn-1)//n
print(long_to_bytes(m))

关于脚本也有几点需要备注的

$rn$对应$r^nmod\ n$

而为什么这么运算

1
2
3
x1 = rn % p
d1 = inverse(q, p-1)
r1 = pow(x1, d1, p)

原因是：

中国剩余定理的利用:

（我觉得有点问题但是能算出来说明是对的）

原脚本r = CRT([p, q], [r1, r2])

说明

或者

但是我不知道怎么得到了噢= =

然而我根据他的思路

所以接下来我们需要由$ r^n mod n$ 得到 $r$ 的值或者 $r^n mod n^2$的值，才可以对 $ r^n $ 在模 $n^2$ 下求逆元。这里可以将 $r^n mod n$ 分别对 $n$ 的两个因数 $p,q$取模，然后再用中国剩余定理（CRT）合起来，从而得到 $r$。

我们可以这么算一下：

利用这两个式子求出$r^n$，再求出$r^n\ mod \ n*n$

试一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from Crypto.Util.number import long_to_bytes, inverse
import gmpy2
from functools import reduce
c = 29088911054711509252215615231015162998042579425917914434962376243477176757448053722602422672251758332052330100944900171067962180230120924963561223495629695702541446456981441239486190458125750543542379899722558637306740763104274377031599875275807723323394379557227060332005571272240560453811389162371812183549
n = 6401013954612445818165507289870580041358569258817613282142852881965884799988941535910939664068503367303343695466899335792545332690862283029809823423608093
p = 80006336965345725157774618059504992841841040207998249416678435780577798937819
q = 80006336965345725157774618059504992841841040207998249416678435780577798937447

def CRT(m, a):
    Num = len(m)
    M = reduce(lambda x, y: x*y, m)
    Mi = [M//i for i in m]
    t = [inverse(Mi[i], m[i]) for i in range(Num)]
    x = 0
    for i in range(Num):
        x += a[i]*t[i]*Mi[i]
    return x % M

rnn=c%n
x1=rnn%p
x2=rnn%q
rn = CRT([p, q], [x1, x2])

print (rn)
R=rn%(n*n)
R_inv = inverse(R, n*n)
mn = (c*R_inv) % (n*n)
m = (mn-1)//n
print(long_to_bytes(m))

但很可惜结果不对…

再挖一坑有空再填

ComplexEncode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
from Crypto.Util.number import *
from flag import FLAG,false_flag
import gmpy2
import random
import hashlib
import base64

def rsaEncode(msg):
    f=open("out","a")
    while True:
        ran=random.randint(3, 12)
        if isPrime(ran):
            break
    e=ran*getPrime(30)
    p = getPrime(1024)
    q = getPrime(1024)
    while (not gmpy2.gcd((p-1)*(q-1),e)==ran or p*q<pow(msg,ran)):
        p = getPrime(1024)
        q = getPrime(1024)
    n=p*q
    assert(pow(msg,ran)<n)
    print("rsaEncode_init_finish!")
    dsaEncode(p)
    f.write("rsaEncode n:"+hex(n)+"\n")
    f.write("rsaEncode e:"+hex(e)+"\n")
    c=pow(msg,e,n)
    f.write("rsaEncode flag is:"+hex(c)+"\n")
    f.close()

def rsaEncode2(m):
    m=int.from_bytes(m.encode(),'big')
    f=open("out","w")
    while True:
        ran=random.randint(20, 50)
        if isPrime(ran):
            break
    e=ran*getPrime(30)
    p = getPrime(1024)
    q = gmpy2.next_prime(p)
    while (not gmpy2.gcd((p-1)*(q-1),e)==ran or p*q>pow(m,ran)):
        p = getPrime(1024)
        q = gmpy2.next_prime(p)
    n=p*q
    assert(pow(m,ran)>n)
    c=pow(m,e,n)
    f.write("n2:"+hex(n)+"\n")
    f.write("e2:"+hex(e)+"\n")
    f.write("rsaEncode2 re is:"+hex(c)+"\n")
    f.close()
    print("rsaEncode2_finish!")
    return pow(m,ran,n)

def dsaEncode(p):
    key=genkey(p)
    (r,s,k,q)=sign(rsaEncode2(false_flag),key)
    sig= r.to_bytes(205, 'big') + s.to_bytes(205, 'big') + k.to_bytes(205, 'big')+ q.to_bytes(205, 'big')
    f=open("out","a")
    f.write("dsaEncode :"+base64.b64encode(sig).decode()+"\n")
    f.close()

def genkey(x):
    # DSA
    N=1024
    L=2048-N-1
    while True:
        q = getPrime(N)
        if q-1>x:
            break
    assert(q-1>x)
    while True:
        t = random.getrandbits(L)
        p = (t * 2*q + 1)
        if isPrime(p):
            break
    e = (p-1) // q
    g = pow(2, e, p)
    y = pow(g, x, p)
    print("genkey_finish!")
    return {'y':y, 'g':g, 'p':p, 'q':q, 'x':x}

def sign(m, key):
    g, p, q, x = key['g'], key['p'], key['q'], key['x']
    k = random.randint(1, q-1)
    Hm = int.from_bytes(hashlib.md5(str(m).encode('utf-8')).hexdigest().encode(), 'big')
    r = pow(g, k, p) % q
    s = (inverse(k, q) * (Hm + x*r)) % q
    return (r, s, k, q)

if __name__ == "__main__":
    msg=int.from_bytes(FLAG.encode(),'big')
    rsaEncode(msg)

还是算汇总几个密码算法的简单题，主要就是看懂这段代码的加密过程

1
2
msg=int.from_bytes(FLAG.encode(),'big')
rsaEncode(msg)

将flag转成整形，然后用rsaEncode函数加密，看一下rsaEncode函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def rsaEncode(msg):
    f=open("out","a")
    while True:
        ran=random.randint(3, 12)
        if isPrime(ran):
            break
    e=ran*getPrime(30)
    p = getPrime(1024)
    q = getPrime(1024)
    while (not gmpy2.gcd((p-1)*(q-1),e)==ran or p*q<pow(msg,ran)):
        p = getPrime(1024)
        q = getPrime(1024)
    n=p*q
    assert(pow(msg,ran)<n)
    print("rsaEncode_init_finish!")
    dsaEncode(p)
    f.write("rsaEncode n:"+hex(n)+"\n")
    f.write("rsaEncode e:"+hex(e)+"\n")
    c=pow(msg,e,n)
    f.write("rsaEncode flag is:"+hex(c)+"\n")
    f.close()

赋值一个素数ran，范围在3到12之间，e为ran乘一个30位的素数，p和q为1024位的大素数
接下来这个while循环就有意思了
只要gmpy2.gcd((p-1)(q-1),e)不为ran 或者 pq<pow(msg,ran) 就继续循环，直到找到这个p和q
所以输出的pow(msg,ran)<pq 且 gmpy2.gcd((p-1)(q-1),e)==ran

接下来dsaEncode(p)，对p进行了dsa加密
c=pow(msg,e,n) 常规的rsa加密

跟进到dsaEncode(p)函数

1
2
3
4
5
6
7
def dsaEncode(p):
    key=genkey(p)
    (r,s,k,q)=sign(rsaEncode2(false_flag),key)
    sig= r.to_bytes(205, 'big') + s.to_bytes(205, 'big') + k.to_bytes(205, 'big')+ q.to_bytes(205, 'big')
    f=open("out","a")
    f.write("dsaEncode :"+base64.b64encode(sig).decode()+"\n")
    f.close()

根据p生成了key，key是{'y':y, 'g':g, 'p':p, 'q':q, 'x':x}
然后再对false_flag进行了rsaEncode2，再用key签名

看看rsaEncode2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def rsaEncode2(m):
    m=int.from_bytes(m.encode(),'big')
    f=open("out","w")
    while True:
        ran=random.randint(20, 50)
        if isPrime(ran):
            break
    e=ran*getPrime(30)
    p = getPrime(1024)
    q = gmpy2.next_prime(p)
    while (not gmpy2.gcd((p-1)*(q-1),e)==ran or p*q>pow(m,ran)):
        p = getPrime(1024)
        q = gmpy2.next_prime(p)
    n=p*q
    assert(pow(m,ran)>n)
    c=pow(m,e,n)
    f.write("n2:"+hex(n)+"\n")
    f.write("e2:"+hex(e)+"\n")
    f.write("rsaEncode2 re is:"+hex(c)+"\n")
    f.close()
    print("rsaEncode2_finish!")
    return pow(m,ran,n)

这里就是题目的突破口了，ran和e的生成和之前一样，关键是p和q，差值很相近可以直接用yafu分解这里的n2，分解得到的p和q进而可以利用gcd求出这个ran，再求出pow(m,ran,n)，这个就是rsaEncode2(false_flag)的结果
为什么可以求出pow(m,ran,n)呢？
参考之前的wp（RSA——当e与φ(n)不互素时），可以令pow(m,e,n)=pow(m^ran,e//ran,n)，将这个m^ran看作是新的明文，设为x
求得的x就是pow(m,ran,n)
所以此处我们得到了rsaEncode2(false_flag)，代码如下
1
2
3
4
5
6
7
8
e2=int('0x57e6b0c63',16)
n2_p=92038254802992589334836021211021722416892343074988502820738425960842862985591620926198422759102071572852989309010179392091711882907907766877651639325642946829388178711105989373057972159393372729050507806434617955128196692311614810456775707826817847326317108693718175021812398842350298774399748620926186724103
n2_q= 92038254802992589334836021211021722416892343074988502820738425960842862985591620926198422759102071572852989309010179392091711882907907766877651639325642946829388178711105989373057972159393372729050507806434617955128196692311614810456775707826817847326317108693718175021812398842350298774399748620926186723619
ran=41
e2=e2//ran
phi2=(n2_p-1)*(n2_q-1)
d2=gmpy2.invert(e2,phi2)
f1=pow(c2,d2,n2) #即rsaEncode2(false_flag)

接下来我们看看sign函数，怎么签名

1
2
3
4
5
6
7
def sign(m, key):
    g, p, q, x = key['g'], key['p'], key['q'], key['x']
    k = random.randint(1, q-1)
    Hm = int.from_bytes(hashlib.md5(str(m).encode('utf-8')).hexdigest().encode(), 'big')
    r = pow(g, k, p) % q
    s = (inverse(k, q) * (Hm + x*r)) % q
    return (r, s, k, q)

这里是dsa的标准签名，参考：https://www.jarviswang.me/?p=169
也就是把我们的rsaEncode2(false_flag)得到的值进行了md5加密得到了Hm，之后返回了四个值，其中包括了关键的k，有了k我们就可以求出p

J6k6ds.png

x就是p

然后我们就要提取r, s, k, q的值出来

1
2
3
dsas='AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACR4uuC531illQ9yIEW1Ki22kYtZNrX77elRFDZr8EKcnrkZC+yyMxlxFNsCrFqEPhGzAPXS++Aa248WMv1uZDNIzi84jiMw7ZWS82OKEwzy0ozV7lEa7deI+QoVdl49kXx3ZVaR2/TrXrfr3dkiBQyORp/DPsSQdkdLoCmtgNycQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAmkIjVBdkWLaqnSz0OdPi69RsjMwT1wVxq81vfDFnOO+JYKfG0OiAZEeJoSeParez6jBH0+RLVc4f6xOFgZcDYopkzR8ZNYlJR78oWmi/0cuxt4nYTTVirtUux3JrT75YQ/+bWmhswBMHQeIAttvqoZp/YZPOmHZdDkl7arrdZ5UAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEt+f1ID5QKI6NEqnVMMputnxfuIs4hCKZbPCEeV6uGoLJSbKaxBlzaO37bTzINBAxCcKQfCsV4ZwZFpTmozZ/dSdoKnIq/tcPh++80pUAjSjVI/rVInJi4CKgaeaf/8MX8ajCImkLJt6N4pA109eZ6TVJDFnbSRRY9P5i5iF2XwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACh5RoGbxvmvqT2pj93NhFj5UruyVjoxCkyw5kD2qEVCfKXZT1ysK9F5A2MJuU1qLKiJ76ATUVid1dtanCzd8XzkzfdY3nEtxqJ4CEJTSnIuthBz4ETBd8+v2+Oc4nTaimIdhQrEtI5M2z9+tq+uQ/qaXbg735CQiU7jjyALgOCoQ=='
print(base64.b64decode(dsas))
#b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x91\xe2\xeb\x82\xe7}b\x96T=\xc8\x81\x16\xd4\xa8\xb6\xdaF-d\xda\xd7\xef\xb7\xa5DP\xd9\xaf\xc1\nrz\xe4d/\xb2\xc8\xcce\xc4Sl\n\xb1j\x10\xf8F\xcc\x03\xd7K\xef\x80kn<X\xcb\xf5\xb9\x90\xcd#8\xbc\xe28\x8c\xc3\xb6VK\xcd\x8e(L3\xcbJ3W\xb9Dk\xb7^#\xe4(U\xd9x\xf6E\xf1\xdd\x95ZGo\xd3\xadz\xdf\xafwd\x88\x1429\x1a\x7f\x0c\xfb\x12A\xd9\x1d.\x80\xa6\xb6\x03rq\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x9aB#T\x17dX\xb6\xaa\x9d,\xf49\xd3\xe2\xeb\xd4l\x8c\xcc\x13\xd7\x05q\xab\xcdo|1g8\xef\x89`\xa7\xc6\xd0\xe8\x80dG\x89\xa1\'\x8fj\xb7\xb3\xea0G\xd3\xe4KU\xce\x1f\xeb\x13\x85\x81\x97\x03b\x8ad\xcd\x1f\x195\x89IG\xbf(Zh\xbf\xd1\xcb\xb1\xb7\x89\xd8M5b\xae\xd5.\xc7rkO\xbeXC\xff\x9bZhl\xc0\x13\x07A\xe2\x00\xb6\xdb\xea\xa1\x9a\x7fa\x93\xce\x98v]\x0eI{j\xba\xddg\x95\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00K~\x7fR\x03\xe5\x02\x88\xe8\xd1*\x9dS\x0c\xa6\xebg\xc5\xfb\x88\xb3\x88B)\x96\xcf\x08G\x95\xea\xe1\xa8,\x94\x9b)\xacA\x976\x8e\xdf\xb6\xd3\xcc\x83A\x03\x10\x9c)\x07\xc2\xb1^\x19\xc1\x91iNj3g\xf7Rv\x82\xa7"\xaf\xedp\xf8~\xfb\xcd)P\x08\xd2\x8dR?\xadR\'&.\x02*\x06\x9ei\xff\xfc1\x7f\x1a\x8c"&\x90\xb2m\xe8\xde)\x03]=y\x9e\x93T\x90\xc5\x9d\xb4\x91E\x8fO\xe6.b\x17e\xf0\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xa1\xe5\x1a\x06o\x1b\xe6\xbe\xa4\xf6\xa6?w6\x11c\xe5J\xee\xc9X\xe8\xc4)2\xc3\x99\x03\xda\xa1\x15\t\xf2\x97e=r\xb0\xafE\xe4\r\x8c&\xe55\xa8\xb2\xa2\'\xbe\x80MEbwWmjp\xb3w\xc5\xf3\x937\xddcy\xc4\xb7\x1a\x89\xe0!\tM)\xc8\xba\xd8A\xcf\x81\x13\x05\xdf>\xbfo\x8es\x89\xd3j)\x88v\x14+\x12\xd293l\xfd\xfa\xda\xbe\xb9\x0f\xeaiv\xe0\xef~BB%;\x8e<\x80.\x03\x82\xa1'

我们知道to_bytes如果不满205字节，就会补零填充，我们以0位基准，切分提取四个值，在转成整形
1
2
3
4
5
6
7
8
9
10
11
12
13
# #r.to_bytes(205, 'big') + s.to_bytes(205, 'big') + k.to_bytes(205, 'big')+ q.to_bytes(205, 'big')
# r=b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x91\xe2\xeb\x82\xe7}b\x96T=\xc8\x81\x16\xd4\xa8\xb6\xdaF-d\xda\xd7\xef\xb7\xa5DP\xd9\xaf\xc1\nrz\xe4d/\xb2\xc8\xcce\xc4Sl\n\xb1j\x10\xf8F\xcc\x03\xd7K\xef\x80kn<X\xcb\xf5\xb9\x90\xcd#8\xbc\xe28\x8c\xc3\xb6VK\xcd\x8e(L3\xcbJ3W\xb9Dk\xb7^#\xe4(U\xd9x\xf6E\xf1\xdd\x95ZGo\xd3\xadz\xdf\xafwd\x88\x1429\x1a\x7f\x0c\xfb\x12A\xd9\x1d.\x80\xa6\xb6\x03rq'
# s=b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x9aB#T\x17dX\xb6\xaa\x9d,\xf49\xd3\xe2\xeb\xd4l\x8c\xcc\x13\xd7\x05q\xab\xcdo|1g8\xef\x89`\xa7\xc6\xd0\xe8\x80dG\x89\xa1\'\x8fj\xb7\xb3\xea0G\xd3\xe4KU\xce\x1f\xeb\x13\x85\x81\x97\x03b\x8ad\xcd\x1f\x195\x89IG\xbf(Zh\xbf\xd1\xcb\xb1\xb7\x89\xd8M5b\xae\xd5.\xc7rkO\xbeXC\xff\x9bZhl\xc0\x13\x07A\xe2\x00\xb6\xdb\xea\xa1\x9a\x7fa\x93\xce\x98v]\x0eI{j\xba\xddg\x95'
# k=b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00K~\x7fR\x03\xe5\x02\x88\xe8\xd1*\x9dS\x0c\xa6\xebg\xc5\xfb\x88\xb3\x88B)\x96\xcf\x08G\x95\xea\xe1\xa8,\x94\x9b)\xacA\x976\x8e\xdf\xb6\xd3\xcc\x83A\x03\x10\x9c)\x07\xc2\xb1^\x19\xc1\x91iNj3g\xf7Rv\x82\xa7"\xaf\xedp\xf8~\xfb\xcd)P\x08\xd2\x8dR?\xadR\'&.\x02*\x06\x9ei\xff\xfc1\x7f\x1a\x8c"&\x90\xb2m\xe8\xde)\x03]=y\x9e\x93T\x90\xc5\x9d\xb4\x91E\x8fO\xe6.b\x17e\xf0'
# q=b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xa1\xe5\x1a\x06o\x1b\xe6\xbe\xa4\xf6\xa6?w6\x11c\xe5J\xee\xc9X\xe8\xc4)2\xc3\x99\x03\xda\xa1\x15\t\xf2\x97e=r\xb0\xafE\xe4\r\x8c&\xe55\xa8\xb2\xa2\'\xbe\x80MEbwWmjp\xb3w\xc5\xf3\x937\xddcy\xc4\xb7\x1a\x89\xe0!\tM)\xc8\xba\xd8A\xcf\x81\x13\x05\xdf>\xbfo\x8es\x89\xd3j)\x88v\x14+\x12\xd293l\xfd\xfa\xda\xbe\xb9\x0f\xeaiv\xe0\xef~BB%;\x8e<\x80.\x03\x82\xa1'
r=bytes_to_long(r)
s=bytes_to_long(s)
k=bytes_to_long(k)
q=bytes_to_long(q)
#r=102444918260914485960515803593656316264069896558543767748045943245816490463204473313147395429832916075026026311649763977454471046744529091286030098421361251686596825698355745706175964479701105151417546201923868642009237880256729235848382505965454374745716920833655480554504720664662850531237312582572126204529
#s=108323898286056086264484557562172859592659941517728209114449871694547991549133924499860722352034592004099117956766326680190915008107049586782560663817197951802874855680436813946926042994668133657035897758213925852954473237450059599800406927980814502939104336113843276842305872574993878555111236443318012176277
#k=53013781125497306915492459533428444528312942617065973290553458779787098973595549883715635840270520436192847906470878403996377952490572570631141756139325067570505281652679711641154708496619877076338721762727749382658378305782411860893158703845541176473795908042964684829863093781341028842168306612717701522928
#q=113686484877116147135245142666172434187495627210597203868865118549955747598193227686630443159583536767390607705595639440619639708279113383984927573204387862603446583828648765766295831093188087021302240469550495379046137652835726203757437694409427584766671910267180390324458641227647973332811523622914243134113

我们这里得到了k，也就可以求p
1
2
3
4
5
6
m=7096687392414687807681566964785645564873574601917190998581568386550667329018739259797776326864568687765381440079816449721044545236538423441977746751754813825754970682778877307282795282550266331491153064703269062572120889378041060093675391580077144394755237319606990734843877022645841076656313250742140415555541111463760763347590281217609545738852928572445181357955416584538341583858213804907523206443869947930061237735468622840996602687017058718801489227037218139266802570004247133644202041084124199916578310297785630261027531276582721516387941888602039590077866521538878084013332968268094317500216548755933226692331
Hm = int.from_bytes(hashlib.md5(str(m).encode('utf-8')).hexdigest().encode(), 'big')
#print(Hm)
r_1=gmpy2.invert(r,q)
p=(r_1*(k*s-Hm))%q
print(p)#103030773486942436659654142903041768844236525866077315420280212349105891011479998019985691813994423283314954926516323846142847363751224051148209594215128512810458860209543214947790266589161123092397904977469160422016164042419663403876859442534225766340503698469512307799400684898177977116843033274844620260771

此处m就是rsaEncode2(false_flag)，求得p就完事了，回去rsaEncode函数求q，然后发现和rsaEncode2过程差不多，指数处也要提取公因子，最后因为 assert(pow(msg,ran)<n)，所以求解msg可以直接开五次方根得到flag

总脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from Crypto.Util.number import *
import gmpy2
import random
import hashlib
import base64

n1=int('0x769bf99a95e9f446788300bfc679b04f26498d26ce1f1384ef22a4bc0606d2fdcf4af86b8e9b26003f561532613a8b7bcb09c0009aefc09c5297f53342b9fe111562c0789dfa91ff4def12c7cb551828079418e1244387f392d6f420c04eb8b99278f5dacb6042828dae19c1f6638d46f9601aceee1511bf600ef548db15ea6ce1ae975cd08236fdac7d457ac9fa203c8f7914702c78dc3ef24fa50c32208225096f5af761f9e4c581dfca7dbc2a4062d59196578e0213a8d1d8a05bfe398a3c8c195b3997fb01b930e2c925732ef78fdd39b4e4681ab3fea4d2c4f1a3b935df5d494817e2c8eef72e3f22f1ef80c3455add7206baf92495ae59adaa7f1bfd25',16)
e1=0x12a316381
c1=int('0xa97f8fd2cbf4aa1cae331dc5261c93a8da3c0a4aadd33cf204cdb2e38e3afdd16aed1a23cd911f96ddc7152b14120949235c0f1849999c5eae06932900f0ccb7c19fb3854623dc0bbc9b9b1fe640075d1db0be91f0e45776b959d008edd17cf41c24d711a5c767d10a630eec8d96baf2668a358c3cbe4533e410667748d73725c04113e9c7d4f19d520aab6b3241a96feb54632a6f816efdc3a2d7c28604a25ce9fd3dc1d0210e0c70132618125bf8eae1f73fa48699fb7cffe5721b5b7fc8511d6cec4ecef1a8bca0d8fe29b0856b3648feac3f1020650063c40be606d9faf0004517dfb202dfb9c664a887f366119ef2efcbf84813f9a4ad54e9ad05e20f0',16)
n2=int('0x431a834246a5969d460cee6b7db01ec4e05daffd60d6674fd1cf3ab96544ad788df5ef729eba08fce3d6c237b47b7cbda093fb414672eea6a58bd902c7e73844a85b2626e3f17a2c2b6c6521288925792bfa2a338cf1d2128d771b55bac2a2cc85f95dd68b4463661813c7ed268c1ca203c74b513edf749799acbfd70b656976f81d124c0385f4dfe549185a4853ace927db615c1ce95b8230a504dbdc6db1ff639e9700e6f074432493b6bf1aa349a9cf66a7116a6095803718a5b78d541b7fbf643bed0bbde5a9370f54a457feef2fde1db15012c337385d011c4a601fe092a0b0a503b65efb1d2c70de6883a504d04292e4216e5c586e0df85b00732460f5',16)
e2=int('0x57e6b0c63',16)
c2=int('0x174e74a04d09ee859030c9fa292c266f9de06bf833dcffc5d24a4382251620cac743cf2d500428d5784fc271e610965547675db2716a9ab277395fc565a2d8520b21d4384a525beda292c276b4477852255c910b0dd08374e68e421b137d90c6c8ca98e219a73231eb285707fff221e57a005113ec16ef61bde87bebd69da1d09cccda411242ba7607a470b31e54e79603eb2c568825a7534df24d0e411fa60d96925f3f2cc63e3ab60f1fe51be80009aba3fdfe947365e578f04fd04a1f9e4afb5fc7ccc1ee831622917386c0d7ae00e6f3f4abd818f6e76d9d173a2e53357496441ae140284c8a6cc3aa22232f1a58fc101427236f2c2afc2277470eb83116',16)

n2_p=92038254802992589334836021211021722416892343074988502820738425960842862985591620926198422759102071572852989309010179392091711882907907766877651639325642946829388178711105989373057972159393372729050507806434617955128196692311614810456775707826817847326317108693718175021812398842350298774399748620926186724103
n2_q= 92038254802992589334836021211021722416892343074988502820738425960842862985591620926198422759102071572852989309010179392091711882907907766877651639325642946829388178711105989373057972159393372729050507806434617955128196692311614810456775707826817847326317108693718175021812398842350298774399748620926186723619
phi2=(n2_p-1)*(n2_q-1)
ran=41
e2=e2//ran
phi2=(n2_p-1)*(n2_q-1)
d2=gmpy2.invert(e2,phi2)
fake_flag_rsa2=pow(c2,d2,n2)  #7096687392414687807681566964785645564873574601917190998581568386550667329018739259797776326864568687765381440079816449721044545236538423441977746751754813825754970682778877307282795282550266331491153064703269062572120889378041060093675391580077144394755237319606990734843877022645841076656313250742140415555541111463760763347590281217609545738852928572445181357955416584538341583858213804907523206443869947930061237735468622840996602687017058718801489227037218139266802570004247133644202041084124199916578310297785630261027531276582721516387941888602039590077866521538878084013332968268094317500216548755933226692331

dsas='AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACR4uuC531illQ9yIEW1Ki22kYtZNrX77elRFDZr8EKcnrkZC+yyMxlxFNsCrFqEPhGzAPXS++Aa248WMv1uZDNIzi84jiMw7ZWS82OKEwzy0ozV7lEa7deI+QoVdl49kXx3ZVaR2/TrXrfr3dkiBQyORp/DPsSQdkdLoCmtgNycQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAmkIjVBdkWLaqnSz0OdPi69RsjMwT1wVxq81vfDFnOO+JYKfG0OiAZEeJoSeParez6jBH0+RLVc4f6xOFgZcDYopkzR8ZNYlJR78oWmi/0cuxt4nYTTVirtUux3JrT75YQ/+bWmhswBMHQeIAttvqoZp/YZPOmHZdDkl7arrdZ5UAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEt+f1ID5QKI6NEqnVMMputnxfuIs4hCKZbPCEeV6uGoLJSbKaxBlzaO37bTzINBAxCcKQfCsV4ZwZFpTmozZ/dSdoKnIq/tcPh++80pUAjSjVI/rVInJi4CKgaeaf/8MX8ajCImkLJt6N4pA109eZ6TVJDFnbSRRY9P5i5iF2XwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACh5RoGbxvmvqT2pj93NhFj5UruyVjoxCkyw5kD2qEVCfKXZT1ysK9F5A2MJuU1qLKiJ76ATUVid1dtanCzd8XzkzfdY3nEtxqJ4CEJTSnIuthBz4ETBd8+v2+Oc4nTaimIdhQrEtI5M2z9+tq+uQ/qaXbg735CQiU7jjyALgOCoQ=='
r=b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x91\xe2\xeb\x82\xe7}b\x96T=\xc8\x81\x16\xd4\xa8\xb6\xdaF-d\xda\xd7\xef\xb7\xa5DP\xd9\xaf\xc1\nrz\xe4d/\xb2\xc8\xcce\xc4Sl\n\xb1j\x10\xf8F\xcc\x03\xd7K\xef\x80kn<X\xcb\xf5\xb9\x90\xcd#8\xbc\xe28\x8c\xc3\xb6VK\xcd\x8e(L3\xcbJ3W\xb9Dk\xb7^#\xe4(U\xd9x\xf6E\xf1\xdd\x95ZGo\xd3\xadz\xdf\xafwd\x88\x1429\x1a\x7f\x0c\xfb\x12A\xd9\x1d.\x80\xa6\xb6\x03rq'
s=b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x9aB#T\x17dX\xb6\xaa\x9d,\xf49\xd3\xe2\xeb\xd4l\x8c\xcc\x13\xd7\x05q\xab\xcdo|1g8\xef\x89`\xa7\xc6\xd0\xe8\x80dG\x89\xa1\'\x8fj\xb7\xb3\xea0G\xd3\xe4KU\xce\x1f\xeb\x13\x85\x81\x97\x03b\x8ad\xcd\x1f\x195\x89IG\xbf(Zh\xbf\xd1\xcb\xb1\xb7\x89\xd8M5b\xae\xd5.\xc7rkO\xbeXC\xff\x9bZhl\xc0\x13\x07A\xe2\x00\xb6\xdb\xea\xa1\x9a\x7fa\x93\xce\x98v]\x0eI{j\xba\xddg\x95'
k=b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00K~\x7fR\x03\xe5\x02\x88\xe8\xd1*\x9dS\x0c\xa6\xebg\xc5\xfb\x88\xb3\x88B)\x96\xcf\x08G\x95\xea\xe1\xa8,\x94\x9b)\xacA\x976\x8e\xdf\xb6\xd3\xcc\x83A\x03\x10\x9c)\x07\xc2\xb1^\x19\xc1\x91iNj3g\xf7Rv\x82\xa7"\xaf\xedp\xf8~\xfb\xcd)P\x08\xd2\x8dR?\xadR\'&.\x02*\x06\x9ei\xff\xfc1\x7f\x1a\x8c"&\x90\xb2m\xe8\xde)\x03]=y\x9e\x93T\x90\xc5\x9d\xb4\x91E\x8fO\xe6.b\x17e\xf0'
q=b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xa1\xe5\x1a\x06o\x1b\xe6\xbe\xa4\xf6\xa6?w6\x11c\xe5J\xee\xc9X\xe8\xc4)2\xc3\x99\x03\xda\xa1\x15\t\xf2\x97e=r\xb0\xafE\xe4\r\x8c&\xe55\xa8\xb2\xa2\'\xbe\x80MEbwWmjp\xb3w\xc5\xf3\x937\xddcy\xc4\xb7\x1a\x89\xe0!\tM)\xc8\xba\xd8A\xcf\x81\x13\x05\xdf>\xbfo\x8es\x89\xd3j)\x88v\x14+\x12\xd293l\xfd\xfa\xda\xbe\xb9\x0f\xeaiv\xe0\xef~BB%;\x8e<\x80.\x03\x82\xa1'
r=bytes_to_long(r)
s=bytes_to_long(s)
k=bytes_to_long(k)
q=bytes_to_long(q)

m=7096687392414687807681566964785645564873574601917190998581568386550667329018739259797776326864568687765381440079816449721044545236538423441977746751754813825754970682778877307282795282550266331491153064703269062572120889378041060093675391580077144394755237319606990734843877022645841076656313250742140415555541111463760763347590281217609545738852928572445181357955416584538341583858213804907523206443869947930061237735468622840996602687017058718801489227037218139266802570004247133644202041084124199916578310297785630261027531276582721516387941888602039590077866521538878084013332968268094317500216548755933226692331
Hm = int.from_bytes(hashlib.md5(str(m).encode('utf-8')).hexdigest().encode(), 'big')
r_1=gmpy2.invert(r,q)
p=(r_1*(k*s-Hm))%q

q=n1//p
phi1=(p-1)*(q-1)
e1=5002847105
e11=e1//5
phi1=(p-1)*(q-1)
d1=gmpy2.invert(e11,phi1)
f1=pow(c1,d1,n1)
flag=gmpy2.iroot(f1,5)[0]
print(long_to_bytes(flag))
b'flag{2a4d55342b46289d1f624d3083c5e2de}'

Author：DGZ

原文链接：https://dgz-cyber.github.io/2020/04/25/%E5%AE%89%E6%81%92%E5%9B%9B%E6%9C%88%E8%B5%9B-Crypto/

发表日期：April 25th 2020, 11:21:20 pm

更新日期：April 29th 2020, 10:51:27 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. notrsa
  2. 2. ComplexEncode
Total : 62
2020
2019
Invalid date
Invalid date
Invalid date
Invalid date
Invalid date
Invalid date
2019
Invalid date
2019
Invalid date
AWD Crypto Misc Re Web 杂 None Pwn 晶体 社工 锂离子电池 钙钛矿 毕设 电池 烹饪 光电 待定
Uncategorized