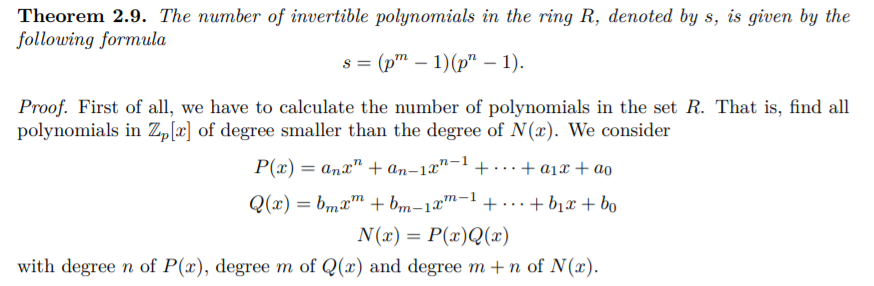基于多项式的RSA

Crypto

Word count: 451Reading time: 2 min

 2020/05/03   Share

要学的东西有点太多，学得又慢，一直看不懂LLL的格要怎么构造，我要吐了。

参考：https://altman.vip/2019/03/25/%E5%9F%BA%E4%BA%8E%E5%A4%9A%E9%A1%B9%E5%BC%8F%E7%9A%84RSA%E4%BD%93%E5%88%B6%E6%8E%A8%E5%AF%BC/

https://github.com/p4-team/ctf/tree/master/2019-03-23-0ctf-quals/crypto_babyrsa

这是去年的一道多项式环的题目，对于当时的我肯定是看半天文章也不知道该怎么求解，现在也还差不多。。。

题目

#!/usr/bin/env sage
# coding=utf-8

from pubkey import P, n, e
from secret import flag
from os import urandom

R.<a> = GF(2^2049)

def encrypt(m):
    global n
    assert len(m) <= 256
    m_int = Integer(m.encode('hex'), 16)
    m_poly = P(R.fetch_int(m_int)) 
    c_poly = pow(m_poly, e, n)
    c_int = R(c_poly).integer_representation() 
    c = format(c_int, '0256x').decode('hex')
    return c

if __name__ == '__main__':
    ptext = flag + os.urandom(256-len(flag))
    ctext = encrypt(ptext)
    with open('flag.enc', 'wb') as f:
        f.write(ctext)

当时做题也只是分解了n，但是直接减1得不到明文，不知道这个欧拉函数要怎么算

而这个题关键在于求不可约多项式的欧拉函数

回到欧拉函数定义本身，欧拉函数是小于或等于n的正整数中与n互质的数的数目。

再看不可约多项式p(x)，除了0，长度为n每一个多项式都与p(x)互素，因此， $φ(p(x))=2^n−1$

同时也可参考：

Polynomial based RSA： http://www.diva-portal.se/smash/get/diva2:823505/FULLTEXT01.pdf

而除了欧拉函数外，其它都和正常的RSA计算过程一致

def decrypt(m, d):
    m_int = Integer(m.encode('hex'), 16)
    m_poly = P(R.fetch_int(m_int))
    c_poly = pow(m_poly, d, n)
    c_int = R(c_poly).integer_representation()
    c = format(c_int, '0256x').decode('hex')
    return c

if __name__ == '__main__':
    p,q = n.factor()
    p,q = p[0],q[0]
    s = (2^p.degree()-1)*(2^q.degree()-1)
    d = inverse_mod(e,s)
    with open('flag.enc', 'rb') as f:
        ctext = f.read()
        print(decrypt(ctext,d))

Author：DGZ

原文链接：https://dgz-cyber.github.io/2020/05/03/%E5%9F%BA%E4%BA%8E%E5%A4%9A%E9%A1%B9%E5%BC%8F%E7%9A%84RSA/

发表日期：May 3rd 2020, 1:15:20 am

更新日期：May 3rd 2020, 1:16:12 am

Next Post

NTRU格密码
Previous Post

深信服培训记录-Misc

CATALOG

