NTRU格密码

Crypto

Word count: 745Reading time: 3 min

 2020/05/03   Share

我就只是想学一下怎么构造格…

参考：https://xz.aliyun.com/t/7163

这是一道巅峰极客线上赛的密码题，这个题目里师傅格构造起来挺友好的。

题目：

from Crypto.Util.number import *
import gmpy2
from flag import flag


def generate():
    p = getStrongPrime(2048)
    while True:
        f = getRandomNBitInteger(1024)
        g = getStrongPrime(768)
        h = gmpy2.invert(f, p) * g % p
        return (p, f, g, h)


def encrypt(plaintext, p, h):
    m = bytes_to_long(plaintext)
    r = getRandomNBitInteger(1024)
    c = (r * h + m) % p
    return c


p, f, g, h = generate()
c = encrypt(flag, p, h)
with open("cipher.txt", "w") as f:
    f.write("h = " + str(h) + "\n")
    f.write("p = " + str(p) + "\n")
    f.write("c = " + str(c) + "\n")

generate函数生成了4个参数p, f, g, h，其中，

p：是一个2048位的强素数

强素数定义：

另外还有述论上的定义，这里应该针对的是密码学

f：一个1024位的随机数。

g：一个768位的强素数。

h：

$h\equiv f^{-1}*g\ (mod\ p)$

这里用全等于号表示因为这里是模运算， $h和f^{-1}*g$ 同余p

而这个h可以看到是在[0,p)这个区间内随机分布的一个数，所以基本是2000多位

encrypt函数对明文（也就是flag）进行了加密：

先生成了一个1024位的随机数r
然后加密：

$c\equiv r*h +m\ (mod\ p)$

我们再来看看给的参数：h, p, c。

显然，如果我们知道了r，那么就可以直接

$m\equiv c-r*h\ (mod\ p)$

解出flag。

但是这里的r是一个随机（本质上是由os.urandom函数）生成的1024-bit数，不可能求得出来的。

如果我们将同余式改写成等式

$c+k*p=r*h+m$

我们来估量一下k的范围：

等式右边r：1024-bit，h：2000多bit，m正常来说几百bit，所以r*h + m大概3000多bit。

相加看最多位，相乘即约等于位数相加，1024+2000 约= 3024

等式左边c：2000多bit，p：2000多bit，因此k大概也有1000多bit，相乘才可以等于右边，所以从k出发也无法求解。

也就是我们无法在有限时间内快速地枚举k求m

所以想要求解，只能在剩下的两个未知参数f, g上作文章了。

假如我们知道了f,g，利用目前已经知道的两个式子

$h\equiv f^{-1}*g\ (mod\ p)$ $c\equiv r*h +m\ (mod\ p)$

我们可以将上式中的h代入下式

$c\equiv r*(f^{-1}*g) +m\ (mod\ p)$

现在假设我们已经知道了f, g，那么只有r, m未知；还是需要知道r才能解出m。

不过我们在式子两边同时乘上f来试试看

$c*f\equiv r*(f^{-1}*g)*f +m*f\ (mod\ p)$

可以得到：

$c*f\equiv r*g +m*f\ (mod\ p)$

我们这时候看看右边的内容

r：1024-bit
g：768-bit
m：flag字符串转成数字，一个字符8bit，一般来说flag不会太长，所以基本上是小于1000bit的。
f：1024-bit
p：2048-bit

所以可以知道右边中 $r*g+m*f<p$

也就是 $r*g+m*f$ 直出直入，没有被模p

如果我们令

$a=c*f\ (mod\ p)$

同样这也是模意义下的求解，需要找到比p小的，所以需要modp

而这时$c*f$大于$p$，我们这时就是看作是一个等式，不看同余式了，此时满足

$c*f\ mod\ p=r*g +m*f$

也就是

$a=r*g +m*f$

于是我们在同余式中找到了一个等式

有了这个式子，就可以帮助我们直接绕过不可爆破求解的r，算出m

对上式子取模g

$a\equiv r*g +m*f \ (mod\ g)$ $a\equiv m*f \ (mod\ g)$

这样，r*g这一项就直接消失了。

其中，a, f, g均已知，求m就很轻松了：

$m\equiv a*f^{-1} \ (mod\ g)$

注意：

这里是在mod g下运算，还记得g是一个768-bit的强素数么？这就保证了，虽然f是个1024-bit的数，但是在mod g下，f' = f - k*g的逆元必定存在。

此处的f^-1与h = f^-1 * g (mod p)里的不是同一个东西。

g有768-bit，768/8=96，flag字符串一般来说不会超过96个字符长，因此m比g小，所以最终算出来的就是完完整整m。

二三句都还挺正常挺好理解的，第一句话想了半天不知道怎么理解

吃个饭的时候突然想到可以这么理解

~~根据一开始维基百科的图，我们知道当g为强素数时，$g=a_3q_3-1~~$

~~而在本题，f是个1024-bit的数，所以如果要逆元存在，就要满足$f*f^{-1}=1+kg~~$

~~我一开始纠结的点在于这个k乘g，里面有个1，这样有个倍数k就消不了1~~

~~但是后面想到f>g~~

~~也就是存在k=1的情况，满足g=f*f^{-1}-1~~

~~此时我们知道f对应$a_3$这个整数，那就存在这个f的逆元~~~~

写完才觉得是狗屁不通，这个k是一定要存在的，但是后面我又想到可以换个思路

如果要满足这个逆元存在，也就是要满足$ff^{-1}=1+kg$存在，也就是$ff^{-1} -kg=1$

而我们根据线性方程定理

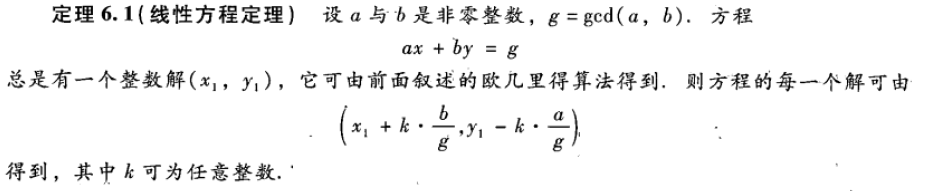
我们把f和g看做a和b，显然gcd（g，f）=1

那么就$f*f^{-1} -kg=1$方程必然有解，也就存在这个逆元

格基规约的利用

上述分析可以知道，我们只要能求出f，g，就能解密

而我们已知可以利用的式子只有：

$h\equiv f^{-1}*g\ (mod\ p)$

我们如何从中求出f, g呢？

这里就是格（Lattice）的范畴了。

先简单介绍一下lattice。

给定一组线性无关的基向量（basis）v1, v2, ..., vn，那么这些基向量的所有线性组合(linear combinations)

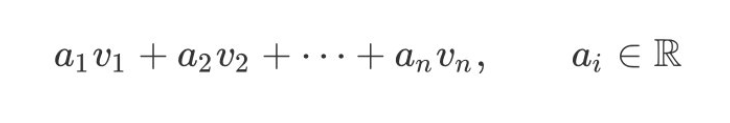
所形成的集合，就叫做这组基向量所张成的空间(span)。

我们在二维平面内选取两个单位正交向量作为基向量$i=(1,0), j=(0,1)$

那么由这两组基向量的所有可能的线性组合张成的空间就是整个二维平面。

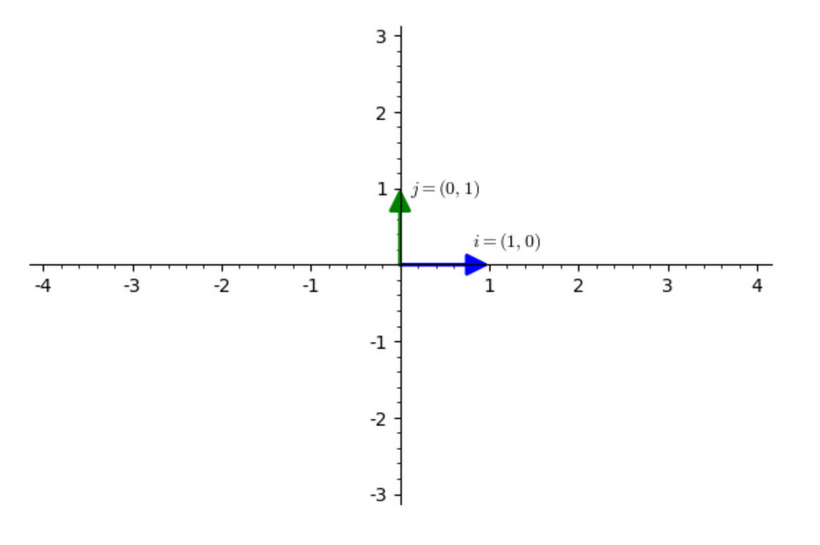
反过来，这个二维平面上的任何一点，都可以由这两组基底的一个线性组合来表示：

其实lattice的定义跟这个差不多。

给定一组线性无关的基向量v1, v2, ..., vn，那么这些基向量的所有整系数线性组合

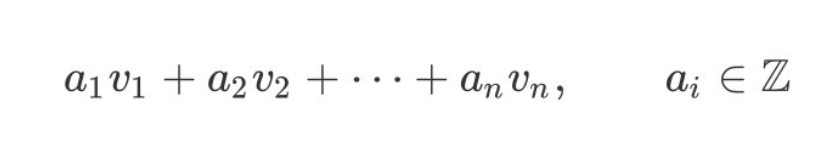
所形成的集合，就叫做这组基向量所张成的格(lattice)，只不过此时的系数只能是整数，也就是说

从无数个连续的点变成了无数个离散的点。不同的基底，可能会张成不同的lattice。对原基底进行

整系数线性转换得到的新的基底，张成的lattice仍旧不变：

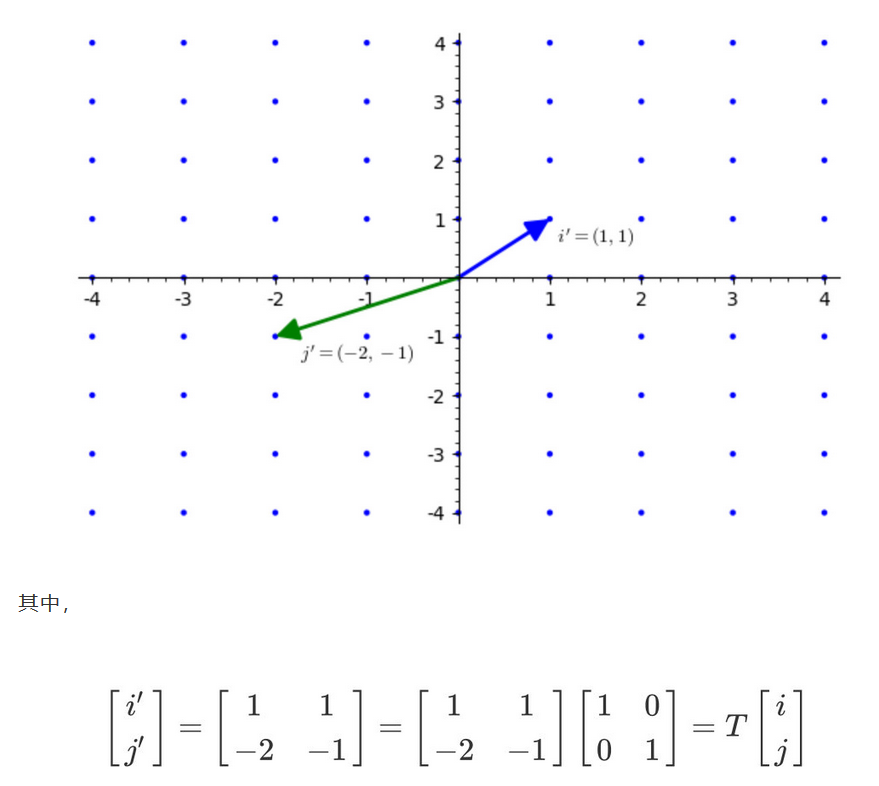
注意：同一个lattice有很多组基底。

在lattice里面，有两个知名的难题：

SVP(最短向量问题，Shortest Vector Problem)：给定lattice和基向量，找到lattice中的一个长度最短的非零向量。
CVP(最近向量问题，Closest Vector Problem)：给定lattice和基向量，以及一个不在lattice上的目标向量，找到lattice中一个距离目标向量最近的格向量。

在广义上的这两大难题已经被证明是NP-hard。

这一题实质上就是一道求解SVP的题目。

虽说，SVP是NP-hard的，但是本题的lattice维度很低，只有2维，所以还是很容易求解的。

实际上，LLL算法及其变种算法是目前已知在较低维度的lattice中求解SVP的最好的算法，但是在较

高维度中就比较乏力。

所以，并不是说NP-hard就不可能求解。

那么，如何将本题看作成一个lattice中求解SVP的题目呢？

对于

$h\equiv f^{-1}*g\ (mod\ p)$

也就是

$h*f\equiv g\ (mod\ p)$

我们可以构造一个由下面这个矩阵M中两个行向量（1，h）（0，p）所长成的lattice：

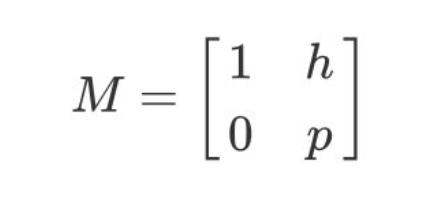
而这和行向量就相当于是这个格的其中一组基，但不是最短的

我们就是要通过格基规约，求解SVP问题，所以我们构造的格，要让想要求解的（f，g）在这个格上，且能通过LLL算法得到

下面我们要先证明向量（f，g）在这个lattice上

向量(f,g)可以由两组基向量M的某种整系数线性组合(f, -u)来表示，因此向量(f,g)就在这个lattice上

我们再来看看h, p, f, g的大小。

h：2000多bit
p：2048-bit
f：1024-bit
g：768-bit

相对于两个基底向量(1, h), (0, p)来说，向量(f, g)的长度要小得多得多：

根据欧几里得范式（其实就是求长度）：

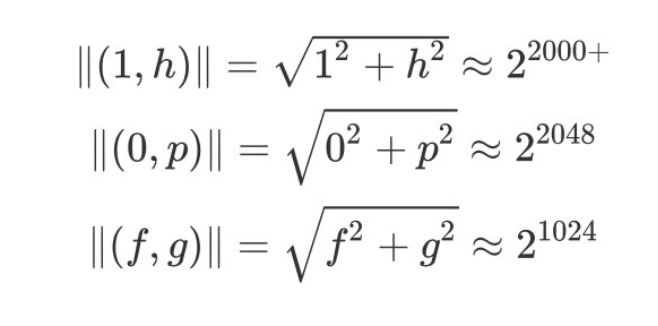
根据Gaussian heurstic可知，在这个lattice中最短向量的长度大概在sqrt(2^2048)=2^1024左右。因此，很大概率上，这个(f, g)就是这个lattice的最短向量。

可见，一开始参数的大小设置，是很关键的一点。

这个参数就是要保证这个(f, g)比自己小，不然就规约不了

（没细究Gaussian heurstic是个啥）

跳过原文自己写的算法，(f, g)就是一个在特定的2维lattice上的最短向量，直接LLL，

h = 7257231567493321493497732423756001924698993879741072696808433246581786362611889417289029671240997843541696187487722285762633068287623369923457879458577466240950224087015909821079480431797917376609839097610864517760515986973340148901898582075413756737310797402537478388864632901178463429574227279668004092519322204990617969134092793157225082977967228366838748193084097651575835471869030934527383379794480007872562067799484905159381690179011192017159985260435844246766711550315143517066359521598424992244464723490166447105679062078049379153154659732304112563255058750656946353654402824529058734270363154894216317570784
p = 23969137365202547728693945383611572667294904799854243194734466236017441545927679469239814785947383727854265554138290421827510545078908517696536495567625593439996528098119344504866817224169113920532528233185011693829122447604993468817512696036673804626830507903206709121383065701222707251053362179946170981868061834734684494881504724254812067180384269711822738708203454131838741703416329765575995359232573740932069147491776326045743679105041246906081872936901848272288949389026129761726749334006319072981386763830897454245553866145620689939497868469730297795063648030738668273210516497399954626983672357236110363894081
c = 6388077150013017095358415295704360631706672647932184267739118115740221804173068089559645506533240372483689997499821300861865955720630884024099415936433339512125910973936154713306915269365877588850574948033131161679256849814325373882706559635563285860782658950169507940368219930971600522754831612134153314448445006958300840618894359885321144158064446236744722180819829183828290798747455324761671198097712539900569386477647697973195787663298318786718012522378981137877863153067057280649127202971806609339007027052518049995341356359016898069863799529357397514218249272201695539181908803360181347114492616706419618151757

# Solve SVP.
v1 = vector(ZZ, [1, h])
v2 = vector(ZZ, [0, p])
m = matrix([v1,v2]);
shortest_vector = m.LLL()[0]
#第二个解[1]是负值
# shortest_vector = GaussLatticeReduction(v1, v2)[0]
f, g = shortest_vector
print(f, g)

# Decrypt.
a = f*c % p % g
m = a * inverse_mod(f, g) % g
print(m)
#print(libnum.n2s(m))
#print(hex(m).decode('hex'))
#在本地如果装了库就可以 在sagecell会报错因

也就是关键的要让所要求的解在我们想要的格以svp最短向量求解得到

Author：DGZ

原文链接：https://dgz-cyber.github.io/2020/05/03/NTRU%E6%A0%BC%E5%AF%86%E7%A0%81/

发表日期：May 3rd 2020, 4:49:20 pm

更新日期：May 8th 2020, 5:13:58 pm

Next Post

格构造学习
Previous Post

基于多项式的RSA

CATALOG

1. 格基规约的利用

