格构造学习

来自菜狗的学习格基规约的一天

算是有一丢丢进步，但后面发现似乎不太对劲

参考：Mathematics of Public Key Cryptography

谷歌直接一搜就有pdf版本

主要章节： Chapter 19 Coppersmith’s Method and Related Applications

我们知道Coppersmith主要是推广了LLL算法对RSA进行攻击

他提出了一个关键的点，对于求解多项式模方程

这里的根$|x_0|$有个约束条件，需要$|x_0|<M^{1/d}$

这里的d是多项式的最高次数

可以通过Howgrave-Graham定理去将这个模方程转换成一个多项式方程

对这个方程求解就可以得到原来的模方程的解，求得的解叫做原模方程的小根，而且这个多项式的

各项系数是比较小的。

例子1：令M=17·19=323，并让

如果我们想要找到模方程$F(x)\equiv 0(mod\ M)$的小根（假设我们知道了这个模方程有个解$x_0=3$），我们可以找到一个多项式$G(x)$

这个多项式满足$G(3)=0$，而进一步的求根可以通过牛顿迭代法（Newton’s method）求根

我们将这个多项式$F(x)$与转变成行向量的形式，与矩阵联系在一起

其中X是小根的上界，这里是为了下面构造格而铺垫

介绍一下Howgrave-Graham提到的其中一个定理

如果满足$||b_F||<M\sqrt{d+1}$，那么$F(x_0)=0$

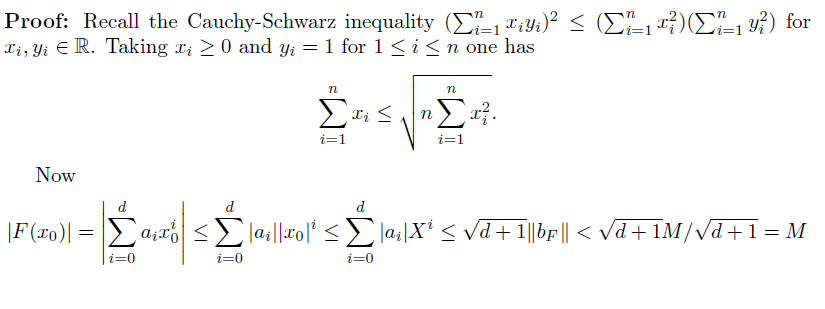
所以$-M<F(x_0)<M$，但是已经有$F(X_0)\equiv 0(mod\ M)$，所以$F(x_0)=0$

其中$||向量||$表示

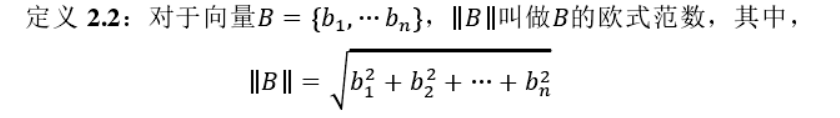
但是另外的一个关键的点，我们要求$F(x_0)$是首一多项式，才可以更加有效地找到这个有相同根的多项式$G(x_0)$，而且有更小的系数。

我们考虑这d+1个多项式：$G_i(x)=Mx^i$和$F(x)$，其中$0\leq i<d $

它们都有对于模M的情况下

都有根

我们定义一个格L，这个格有着以这些多项式构成的格基

因此这个格L可以用下面的矩阵表示

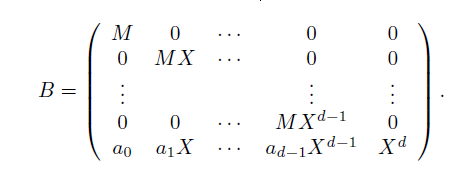
构成一个d+1阶的对角矩阵

我们一般情况下都想通过扩大根的上界，以趋近无约束条件下的求根，比如对于多项式模方程$F(x)\equiv 0(mod\ M)$，最理想的根的上界就是M，但是这个不现实的。

而对于LLL算法，他有个优点可以让这个小根有着更大的约束范围（有个定理进一步约束了X的值）

例子二：令M=10001，并让

我们可以确定这个多项式是不可约的，如果可以约的话，将进一步简化这个问题，我们令X=10，根据刚才的理解构造一个格：

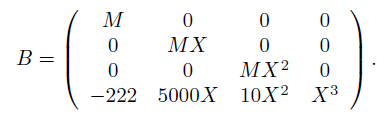
在sage上利用自带的LLL算法进行格基规约，可以得到第一个行向量为(444, 10, −2000, −2000).

1
2
3
4

m=10001
x=10
M = matrix([[m,0,0,0],[0, m*x,0,0],[0, 0,m*x*x,0],[-222,5000*x,10*x*x,x*x*x]])
print(M.LLL())

这个行向量对应于：

可以求到根$x_0=4$

代进$F(x)$中确实是满足$F(x_0)\equiv 0(mod\ n)$

而当我们将X的值设为5的时候，结果如下

好的我是智障，py3的异或和幂弄混了

算出来是没错的

而这里sage的small_roots可以一步到位

1
2
3
4
5
6

N = 10001
K = Zmod(10001)
P.<x> = PolynomialRing(K, implementation='NTL')
f = x^3 + 10*x^2 + 5000*x - 222
f.small_roots()
#[4]

这里的NTL可以看成是一个库

下午的时候我还想着问哪个大哥来给我讲讲这个格是怎么构造出来的…我想找到师傅的邮箱去问了…

还好到了晚上居然想到了

说明了洗澡的重要性

最关键的就是最后一个行向量原多项式形式为$F(x)·F(x)$

但是似乎知道了还没什么用？

好气噢zenmexue